04-Self-attention
1. 輸入是向量序列
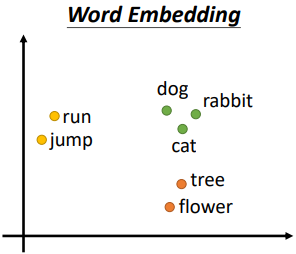
1.1 文字處理(自然語言處理)
將每一個詞彙表示為向量
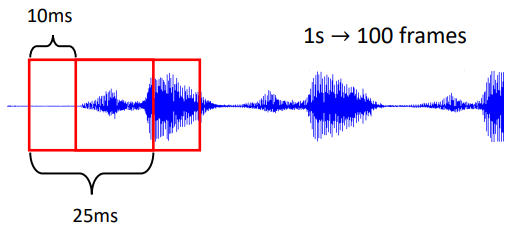
1.2 聲音信號處理
會把一段聲音訊號取一個範圍,這個範圍叫做一個窗口(window),把該窗口裡面的訊息描述成一個向量,這個向量稱為一幀(frame)。一小段的聲音訊號,它裡面包含的訊息量非常可觀
1.3 圖
社交網路是一個圖,在社交網路上面每一個節點就是一個人。每一個節點可以看作是一個向量。每一個人的訊息(性別、年齡及工作等等)都可以用一個向量來表示。因此一個社交網路可以看做是一堆的向量所組成
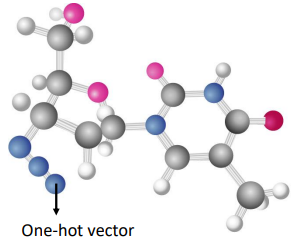
把一個分子當做是模型的輸入,每一個分子可以看作是一個圖,分子上面的每一個球就是一個原子,每個原子就是一個向量,而每個原子可以用獨熱向量來表示
2. 輸出的三種可能性
2.1 每一個向量都有一個對應的標簽
輸入跟輸出的長度是一樣的。模型不需要去煩惱要輸出多少的標簽,輸出多少的標籤

舉例:
- 詞性標註(POS tagging):機器會自動決定每一個詞彙的詞性,判斷該詞是名詞還是動詞還是形容詞等等
- 語音辨識
- 社交網路:每個節點(人)進行標註【是否推送商品】
2.2 一組向量序列輸出一個標簽
整個序列只需要輸出一個標籤就好

舉例:
- 文本情感分析:給機器看一段話,模型要決定這段話是積極的(positive)還是消極的(negative)
- 語音辨識
- 分子的疏水性:給定一個分子,預測該分子的親水性
2.3 模型自行決定輸出多少個標籤
輸入是 N 個向量,輸出可能是 N′ 個標簽,而N′ 是機器自己決定的。此種任務被稱作序列到序列(Sequence to Sequence,Seq2Seq)

舉例:
- 翻譯
- 語音辨識
3. Self-attention 運作原理
3.1 以 Sequence Labeling 為例
考慮第一個輸出可能性,每一個向量都有一個對應的標簽,Sequence Labeling 要給序列裡面的每一個向量一個標簽
方法一
對每一個向量,用 Fully-connected network 分別進行處理
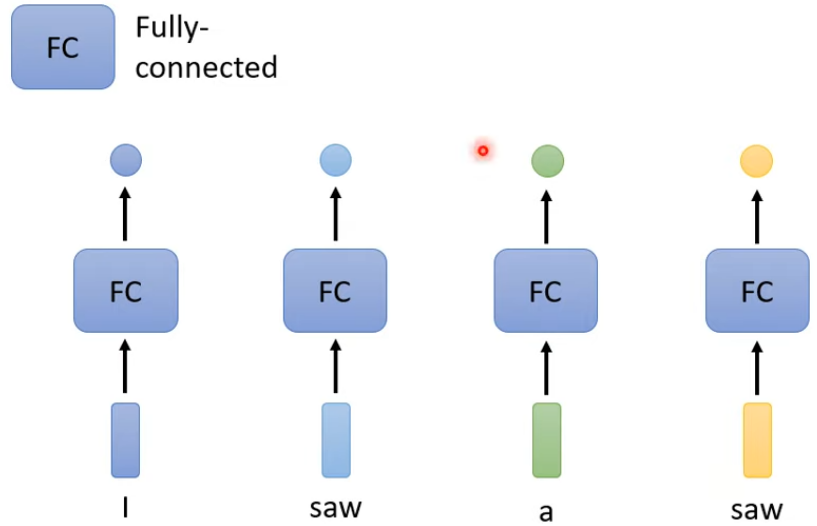
問題:
有非常大的瑕疵,因為忽略了序列上下文的關係。同一個詞彙在句子中不同的位置、不同的上下文環境下,詞彙的詞性有可能是不一樣的,但此方法的輸出會因是同個詞彙而永遠只有同個輸出
方法二
改進方法一串聯若干個向量後丟進 Fully-connected network。給 Fully-connected network 一整個 window 的訊息,讓它可以考慮一些上下文,即與該向量相鄰的其他向量的訊息
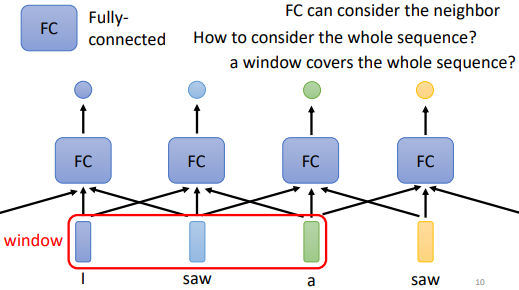
問題:
序列的長度有長有短,輸入給模型的序列的長度,每次可能都不一樣。開一個 window 比最長的序列還要長,才可能把整個序列蓋住。但是開一個大的窗口,意味著 Fully-connected network 需要非常多的參數,可能運算量會很大,此外還容易過擬合
⇒ 想要更好地考慮整個輸入序列的訊息,就要用到自注意力模型
3.2 Self-attention model
考慮整個序列的所有向量,綜合向量序列整體和單個向量個體,得到對每一個向量處理後的向量,將這些向量個別連接一個 FC,FC 可以專注於處理這一個位置的向量,得到對應結果
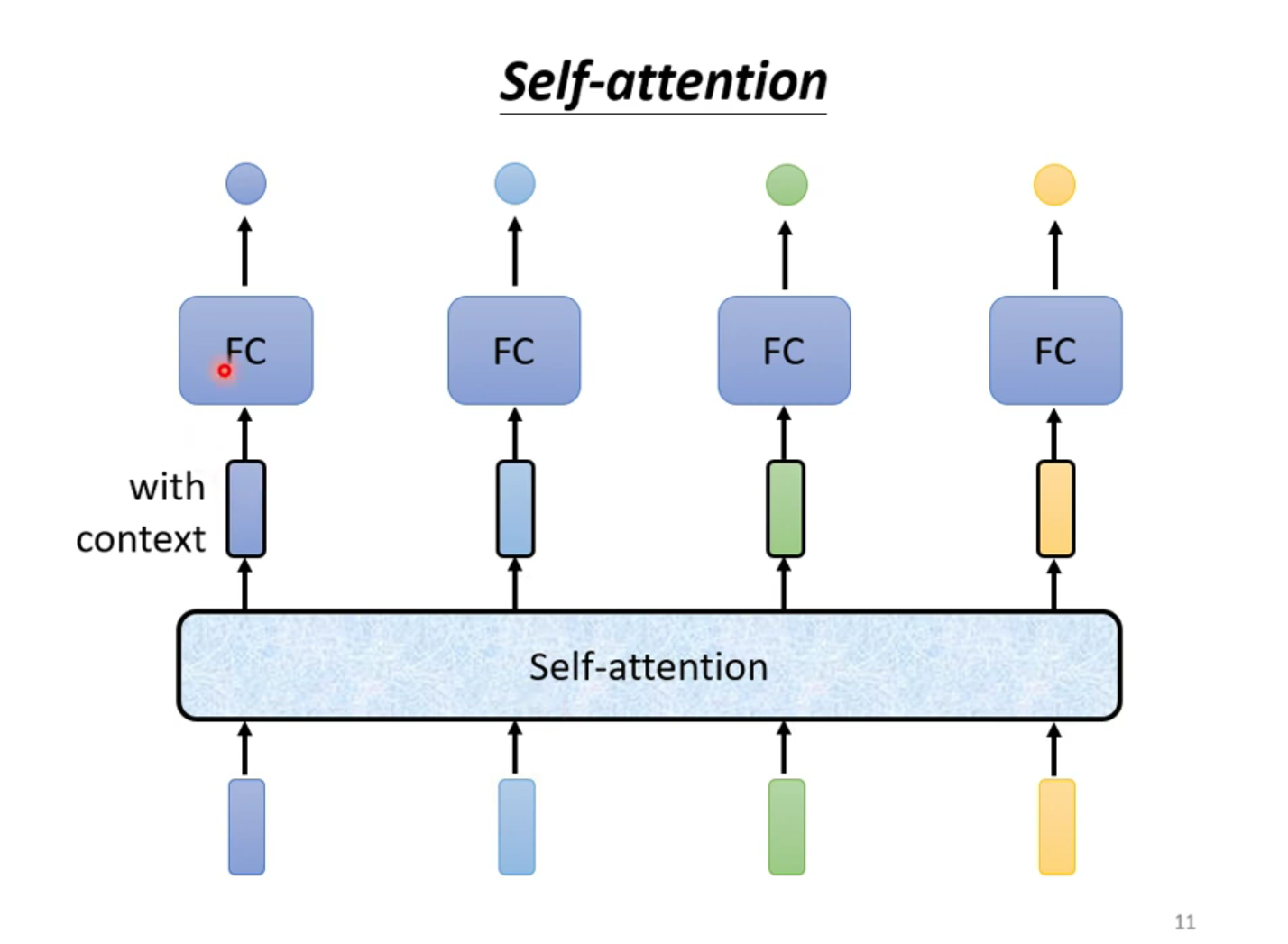
自注意力模型不是只能用一次,可以疊加很多次,與 FC 可以交替使用
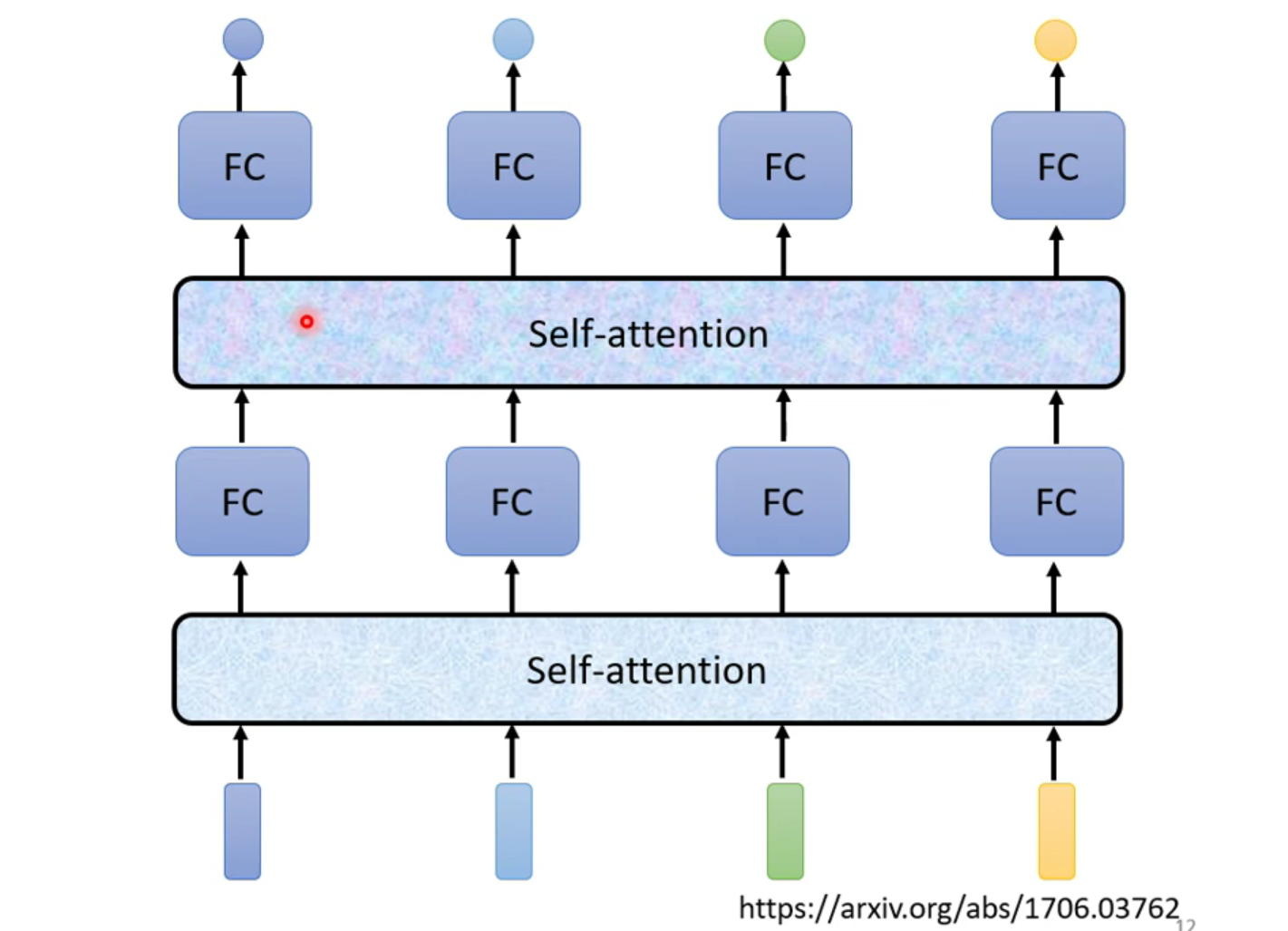
3.1.1 內部架構
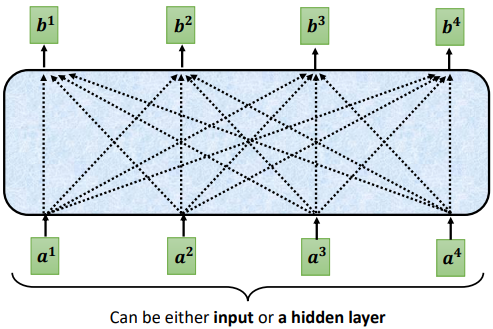
輸入:一串的 vector,這些 vector 可能是整個 network 的 input,也可能是某個 hidden layer 的output
輸出:處理 input 以後,每一個 b 都是考慮了所有的 a 以後才生成出來的
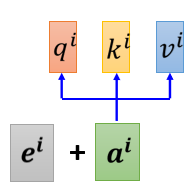
3.1.2 具體步驟
- 根據 向量找出跟其他向量的相關程度
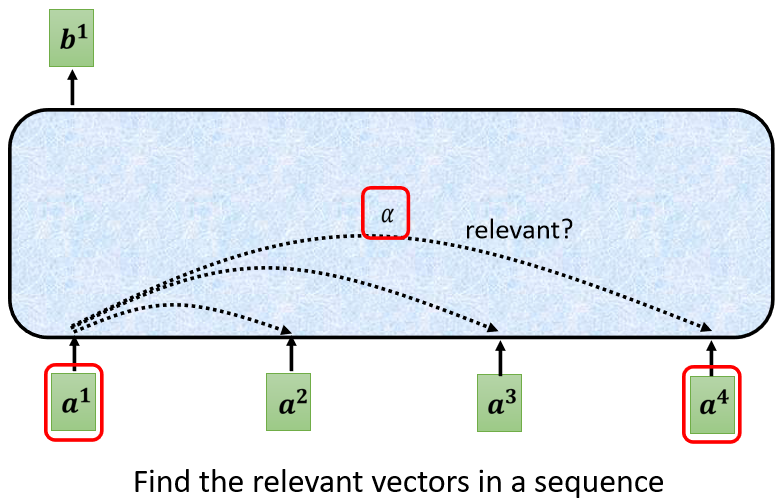
- 藉由一個計算 attention 的模組來得到 α。( = query、 = key)
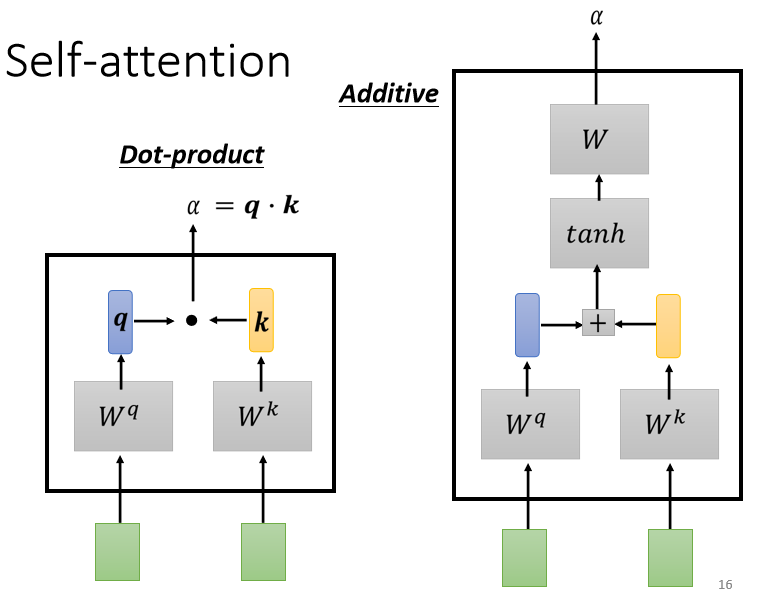
- Dot-product:
把輸入的兩個向量分別乘上 和 ,得到兩個向量 跟 後做點積,把它們做逐元素(element-wise)的相乘, 再全部加起來得到一個 α
(常用,也被用在 Transformer 中)
- Addtive:
兩個向量通過 和 得到 和 後,把 和 串起來丟到 函數(activation function),再乘上矩陣 得到 α
- 計算完 跟其他向量的相關性 後(也必須計算 跟自己的 ),把所有的 經過 softmax (也可使用其他激勵函數,如: ReLu)得到
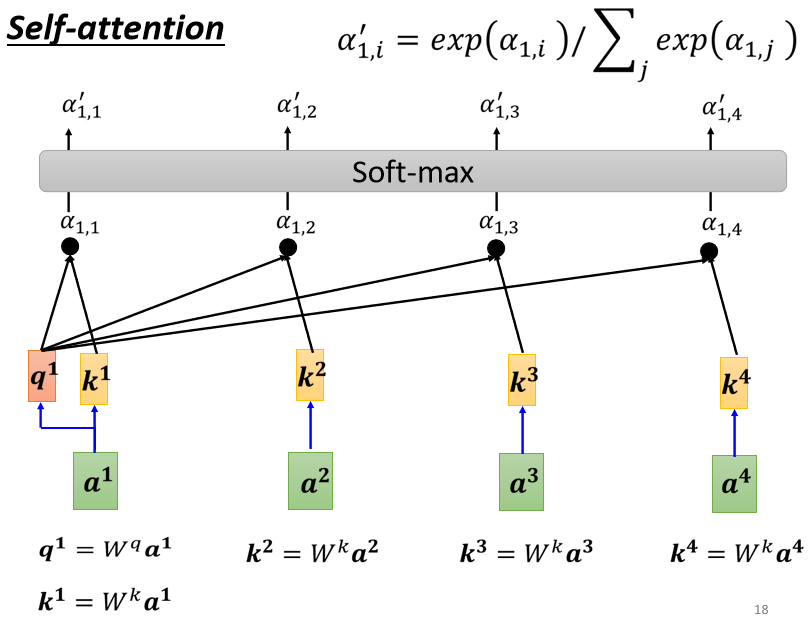
- 把向量 到 乘上 得到新的向量:、、 和 ,接下來把每一個向量都去乘上 後再求和得到
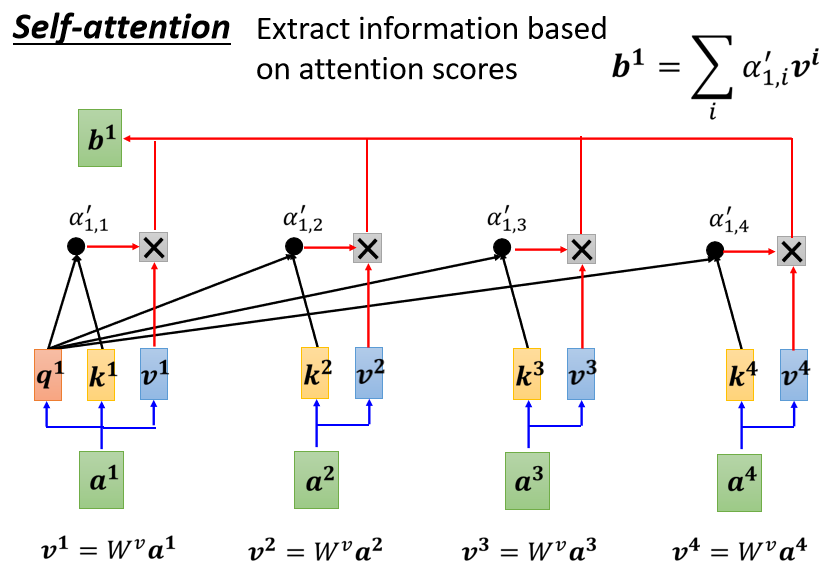
如果 跟 有高相關性,即 的值很大,再做加權和後,得到的 就可能會比較接近 。所以誰的注意力的分數最大,誰的 就會主導(dominant) 抽出來的結果
注意: 到 是同時被計算出來的
3.1.3 矩陣的角度
- 先計算 ,合併後以 表示
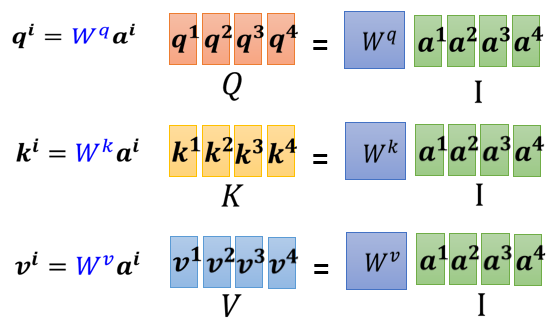
- 根據 計算 經過一激勵函數,如:softmax 或 ReLu,得到 (稱做 attention matrix)

- 再乘以 得到 ,以 表示
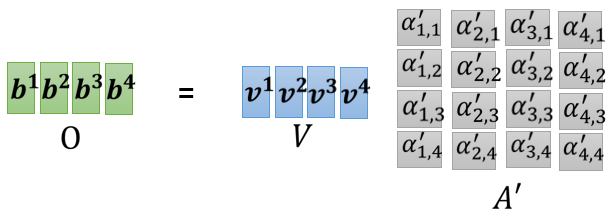
綜合:
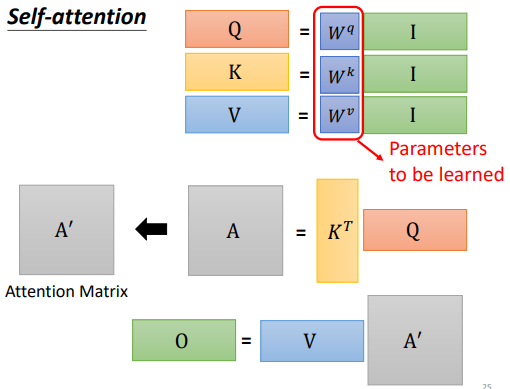
- 每 vector 以 column 併起來稱做 矩陣, 是 Self-attention 的一組 vector input
- 這些 input 分別乘上 矩陣得到
- 接下來 乘上 得到 ,再經過激勵函數得到 稱 Attention Matrix(生成 就是為了得到 attention 的 score)
- 再乘上 ,就得到 。 就是 Self-attention 這個 layer 的輸出
- 是三個要學習的矩陣參數
3.3 Multi-head Self-attention
Multi-head Self-attention 的使用非常廣泛,有一些任務,如翻譯、語音識別等,用該方法可以得到較好的結果。需要多少的 head 是需要調的 hyperparameter
原因:
在使用 Self-attention 計算相關性的時,是用 去找相關的 。但是”相關”有很多種不同的形式,所以也許可以有多個 ,不同的 負責不同種類的相關性,這就是 Multi-head Self-attention
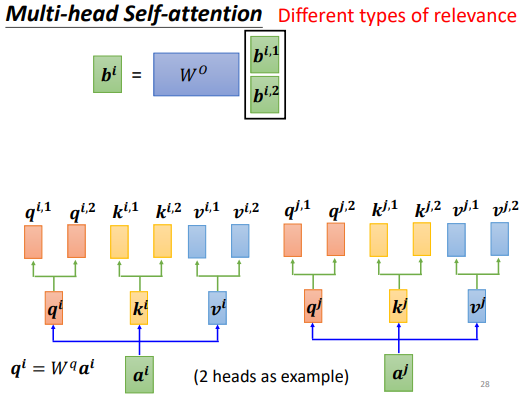
步驟:
- 先把 乘上一個矩陣得到
- 再把 乘上另外兩個矩陣,分別得到 跟 ,代表有兩個 head;同理可以得到 , ,
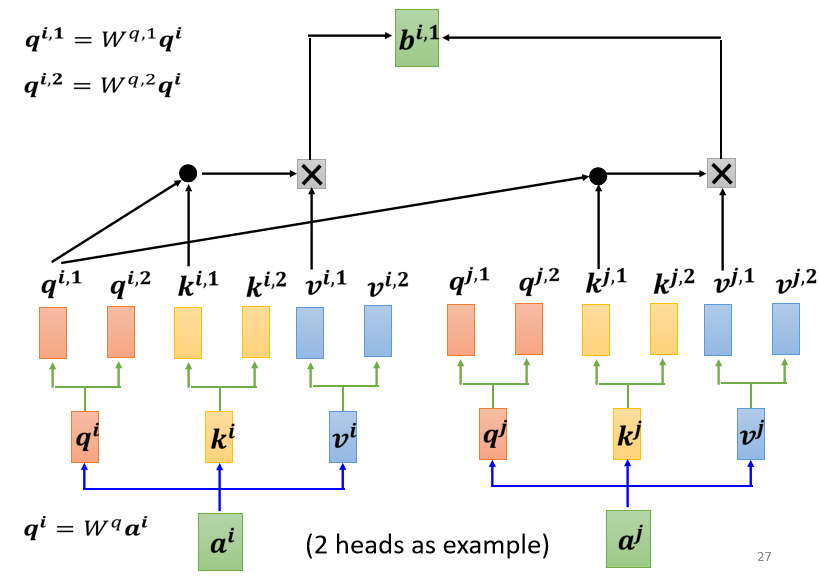
- 從同一個 head 裡的 計算
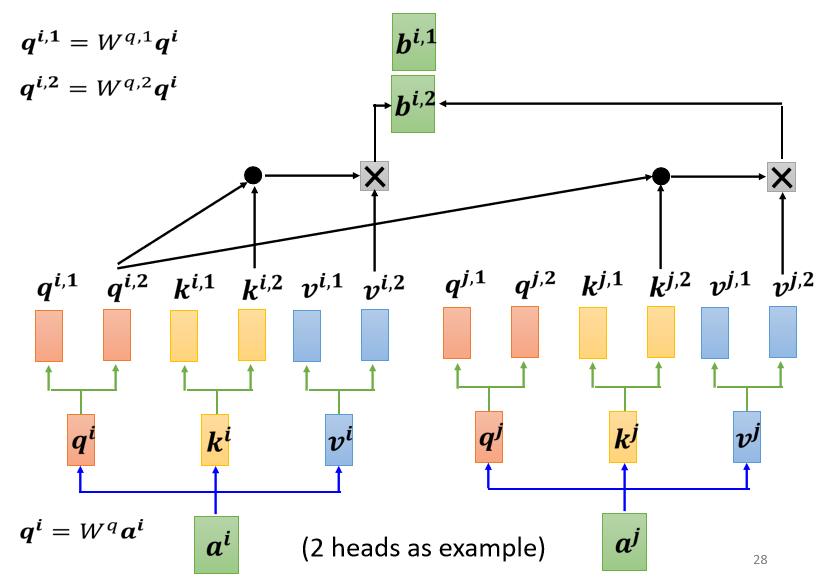
- 將各個 head 計算得到的 拼接,通過一個 transform 得到 然後再送到下一層
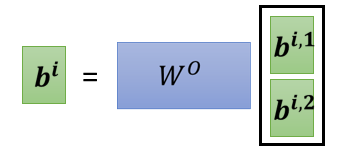
4. Positional Encoding
到目前為止,Self-attention 的操作裡面沒有位置的訊息,但有時候位置的訊息很重要。舉例,在做詞性標註時,動詞較不容易出現在句首,如果某一詞彙是放在句首,其為動詞的可能性就比較低,所以位置的訊息往往也是有用的
方法:
每個位置用一個 vector 来表示它是 sequence 的第 i 個,然後加到原向量中
產生 positional encoding vector 的方法有很多種,如人工設置、根據資料訓練出來等,目前還不知道哪一種方法最好,仍是一個尚待研究的問題
5. 應用
5.1 自然語言處理
在自然語言處理領域,除了 Transformer 外,BERT 也用到了 Self-attention
5.2 語音
問題:
把一段聲音訊號表示成一組向量的話,這組向量可能會非常地長;attention matrix 的計算覆雜度是長度的平方,因此需要很大的計算量、很大的存儲空間
解決方法:
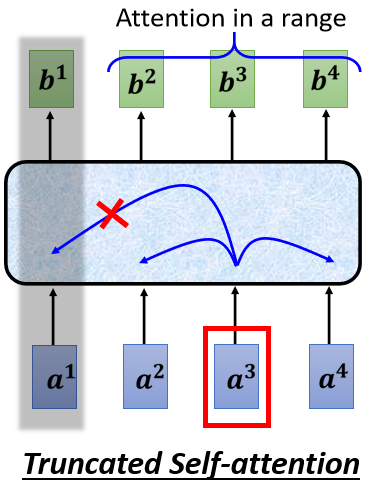
延伸 Self-attention 的概念,運用 Truncated Self-attention。使用 Truncated Self-attention 只考慮一個小範圍語音,而不考慮一整個句子,如此就可以加快運算的速度
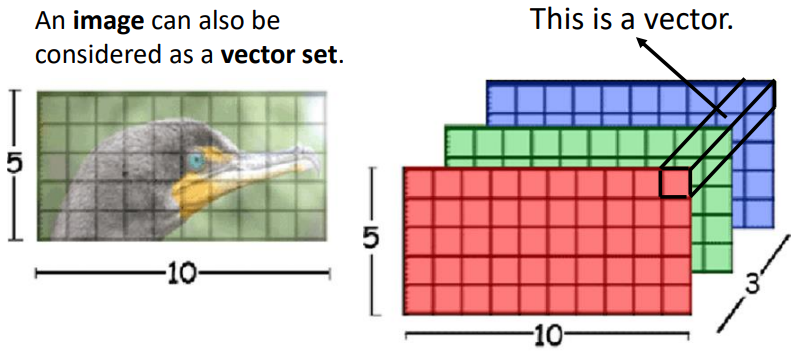
5.3 圖像
一張圖像可以看作是一個向量序列,既然也是一個向量序列,那麼就也可以用 Self-attention 來處理圖像
5.3.1 Self-attention vs CNN
Self-attention:
考慮一個像素和整張圖片的訊息
⇒ 自己學出 receptive field 的形狀和大小
CNN:
receptive field 是人為設定的,只考慮範圍內的訊息
結論:
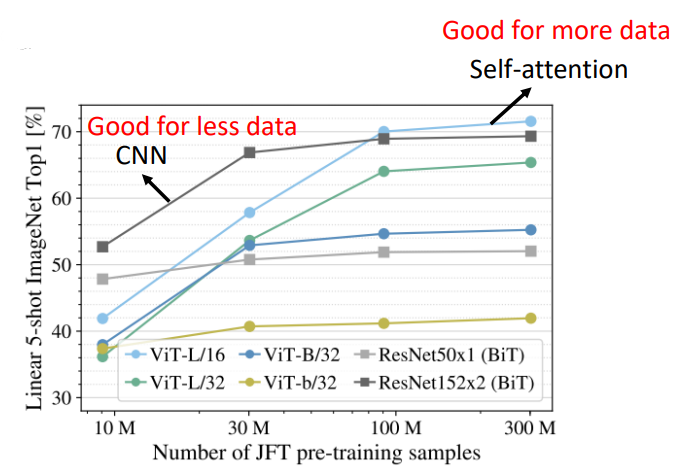
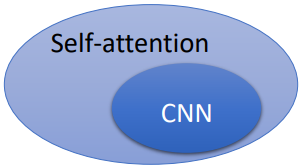
CNN 就是 self-attention 的特例,可說是更 flexible 的 CNN,Self-attention 只要設定合適的參數,它可以做到跟 CNN 一模一樣的事情。根據 An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale 這篇 paper 顯示的結果,給出以下解釋:
- Self-attention 彈性比較大,所以需要比較多的訓練資料,訓練資料少的時候會 overfitting
- 而 CNN 彈性比較小,在訓練資料少時結果比較好,但訓練資料多時,它沒有辦法從更多的訓練資料得到好處
5.3.2 Self-attention vs RNN
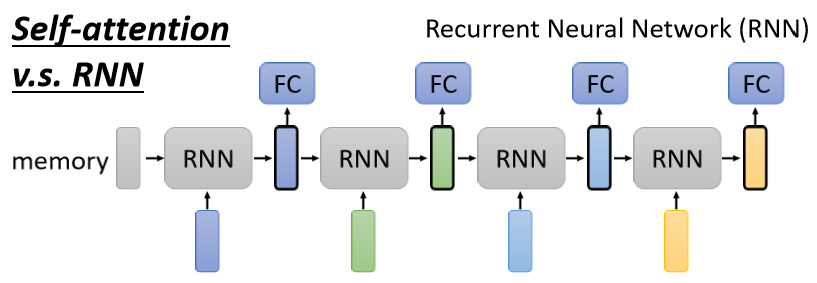
Recurrent Neural Network 跟 Self-attention 做的事情非常像,它們的 input 都是一個 vector sequence,前一個時間點的輸出也會作為輸入丟進 RNN 產生新的向量,也同時會輸入到 FC。很多的應用往往都把 RNN 的架構逐漸改成 Self-attention 的架構
主要區別:
- 對 RNN 來說,假設最右邊黃色的 vector 要考慮最左邊的輸入,那它必須要把最左邊的輸入存在 memory 中都不能夠忘掉一路帶到最右邊,才能夠在最後的時間點被考慮
- 對 Self-attention 來說沒有這個問題,它可以在整個 sequence 上非常遠的 vector之間輕易地抽取訊息
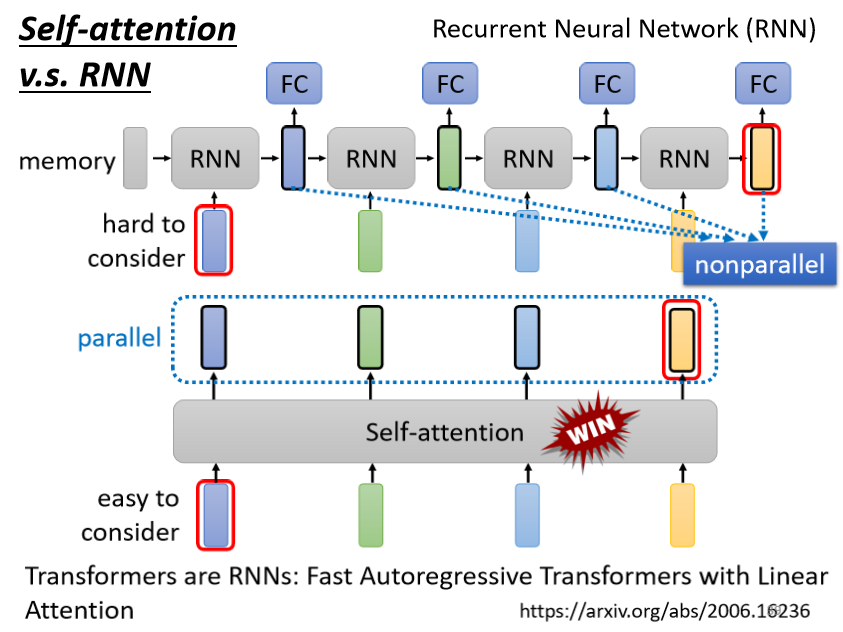
Self-attention 可以平行處理所有的輸出,效率更高:
- Self-attention 四個 vector 是平行產生的,不需等誰先運算完才把其他運算出來
- RNN 無法平行化,必須依次產生
5.4 圖
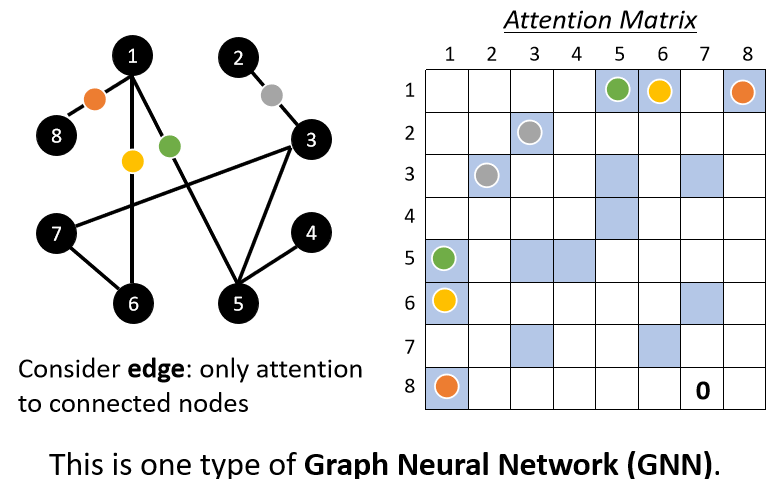
Self-attention 也可以在圖中使用,把 node 當作 vector。然而,圖中的 edge 意味著節點之間的關係,所以我們就可只計算有 edge 相連的 node 的 attention,若兩個 node 之間沒有 edge,代表兩個 node 沒有關係,就不必計算 attention。這種方法也被稱為圖神經網路(GNN)。
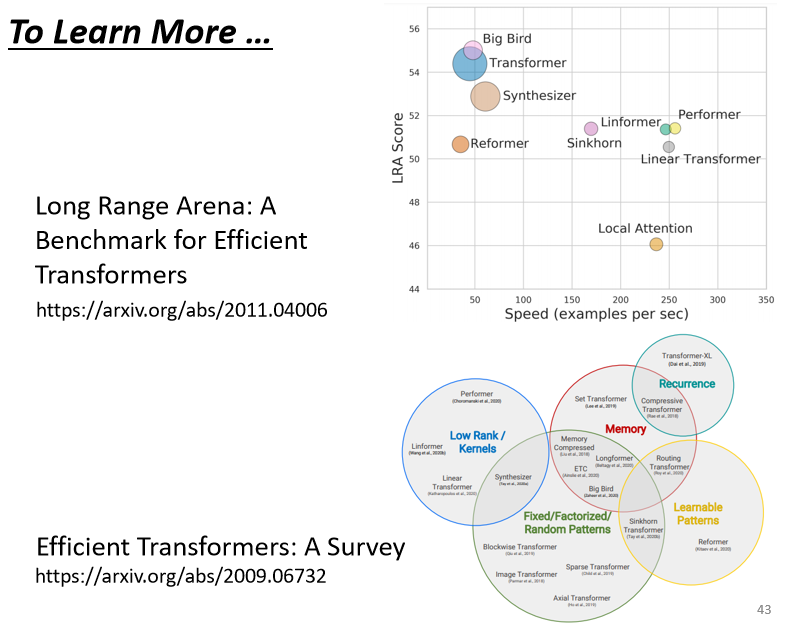
6. Learn More
Self-attention 有多種變形,由於其計算成本高,減少其計算量是未來的研究方向。Long Range Arena: A Benchmark for Efficient Transformers 這篇論文比較了各種不同的自注意力的變形,許多 Self-attention 的變形如:Linformer、Performer、Reformer 等等,往往比原來的 Transformer 性還能差一些,但是速度會比較快。想進一步研究可參考 Efficient Transformers: A Survey 這篇論文