03-CNN(卷積神經網路)
立足點:Network 的架構設計的思想
1. Image Classification
1.1 基本步驟
- 把所有圖片都先 rescale 成大小一樣
- 把每一個類別表示成一個 one-hot vector(dimension 的長度決定模型可以辨識出多少不同種類的東西)
- 將圖片輸入到模型中
1.2 將圖片輸入到模型中
直覺思路會直接展平,但會導致參數量過大
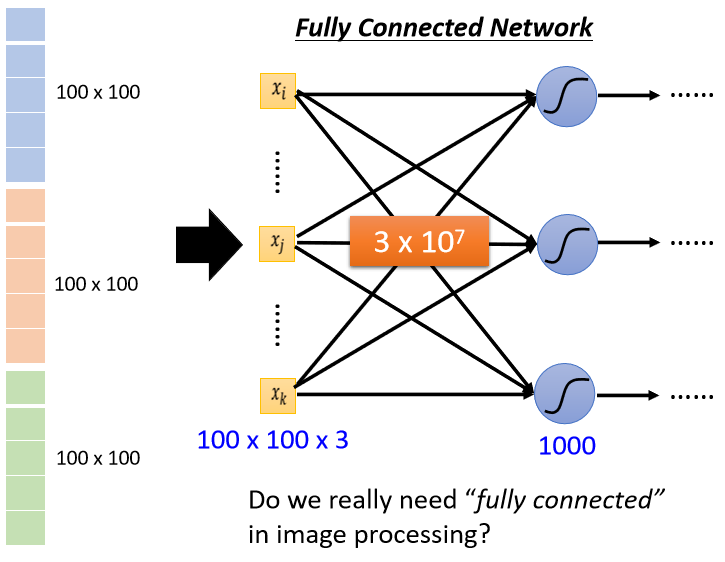
如果輸入的向量長度是 100 × 100 × 3,有 1000 個 neuron,那第一層的 weight 就有 1000 × 100 × 100 × 3,也就是 3×10 的 7 次方,是非常巨大的數目
雖然隨著參數的增加,可以增加模型的彈性,可以增加它的能力,但是也增加了 overfitting 的風險
思考:
考慮到影像辨識問題本身的特性,其實並不一定需要 fully connected,不需要每一個 neuron 與 input 的每一個 dimension 都有一個 weight
2. 神經元角度介紹 CNN
觀察 ①
模型通過識別一些特定 patterns 來識別物體,而非整張圖
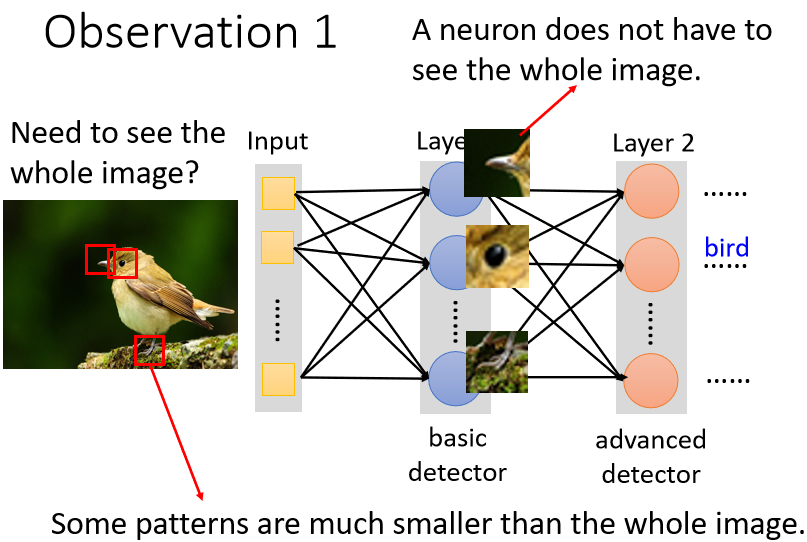
neuron 也許根本不需要把整張圖片當作輸入,只需把圖片的一小部分當作輸入,就足以偵測某些特別關鍵的 pattern 有沒有出現
簡化 ①:Receptive Field
每個神經元只需要考察自己特定範圍內的圖像訊息,將圖像內容展平後輸入到神經元中即可
注意:
- receptive field 之間可以重疊
- 一個 receptive field 可以有多個神經元守備
- receptive field 可以有大有小
- receptive field 可以只考慮某一些 channel
- receptive field 可以是長方形
- receptive field 不一定要相連
Receptive Field 的 Typical Setting(In general)
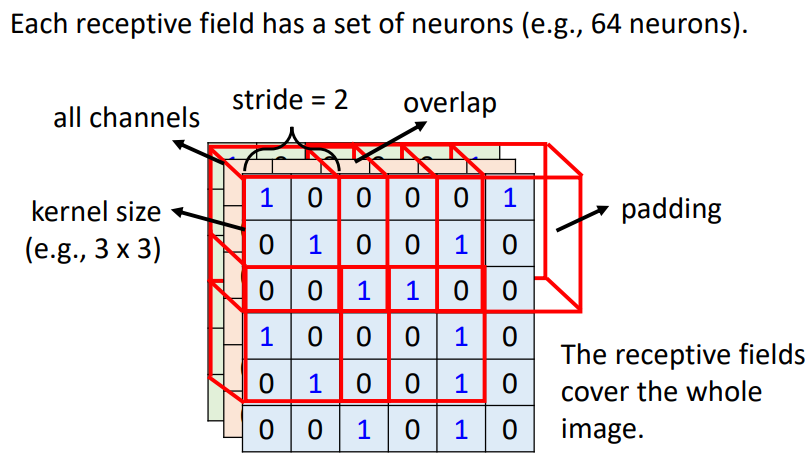
- 一般在做影像辨識的時會看全部的 channel。所以在描述一個 receptive field 的時候,無需說明其 channel 數,只要講它的高、寬 ⇒ kernel size
→ 一般不做過大的 kernal size,常常設定為 3 × 3
- 每個 receptive field 會有不止一個神經元進行守備 ⇒ 輸出通道數/卷積核數目
- 不同的 receptive field 之間的關係 ⇒ receptive field 的水平垂直位移:Stride【hyperparameter】
→ 一般希望 receptive field 之間有重疊,避免交界處的 pattern 被忽略
- receptive field 超出影響的範圍 ⇒ padding(補值:補 0、補平均值、補邊緣值、…)
觀察 ②
同樣的 pattern,可能出現在圖片的不同位置,偵測同樣 pattern 的神經元做的工作是一樣的,儘管守備的 receptive field 不一樣,但參數會是一樣的
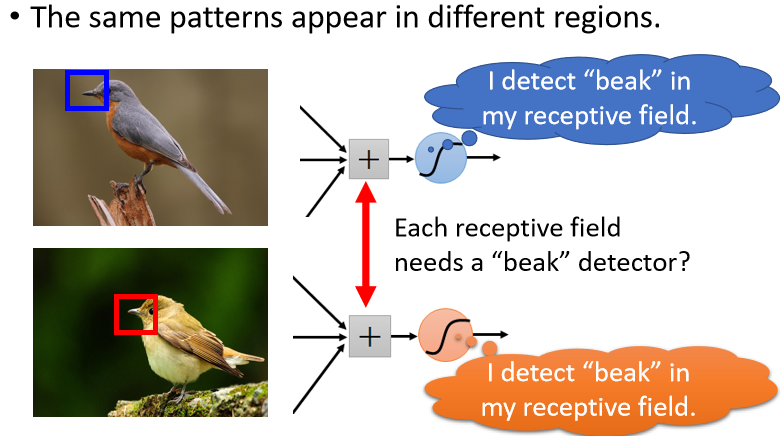
簡化 ②:Parameter Sharing
兩個不同 receptive field 的 neurons 有做一樣的工作,就可以共用參數。儘管參數一樣,但因為是不同的 receptive field(不同的輸入),所以輸出也會是不一樣的
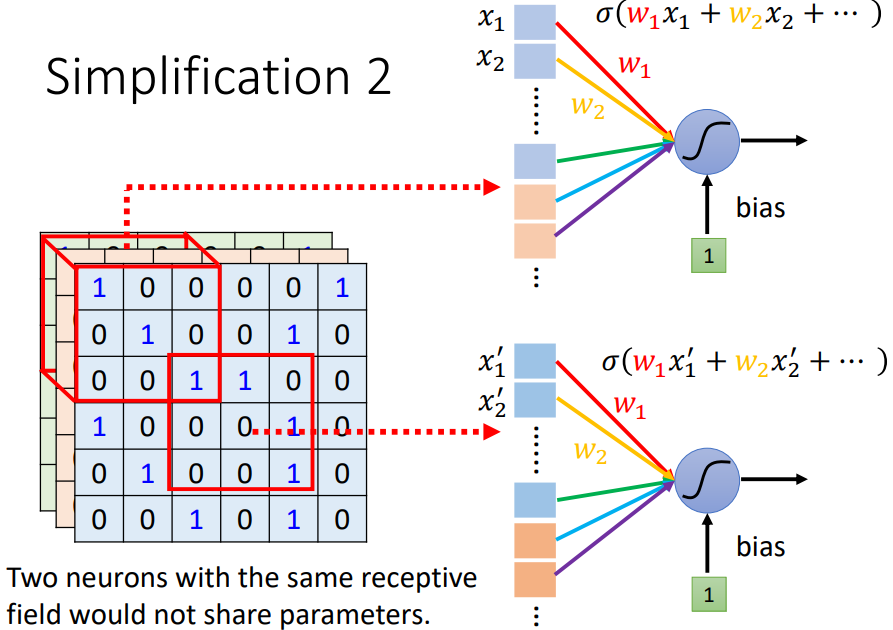
Parameter Sharing 的 Typical Setting(In general)
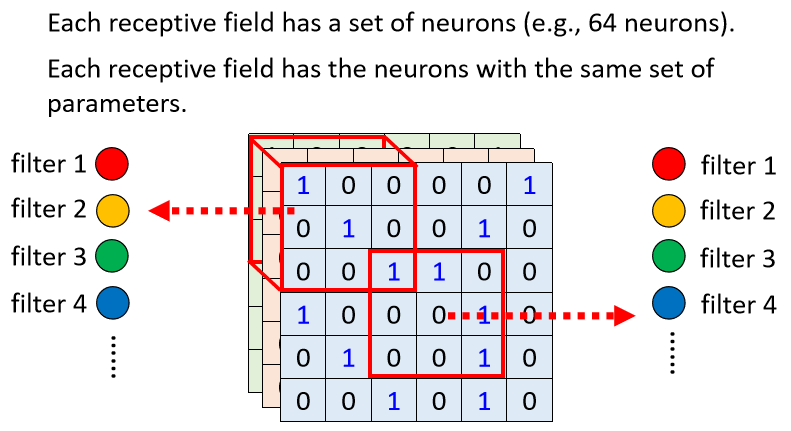
對每個 receptive field,都使用一組神經元處理;這些神經元共用一組參數(weight),此組參數稱作 Filter,因此對不同 receptive field 使用的 Filter 參數相同
Convolutional Layer 的優勢
卷積層是“受限”(彈性變小)的 Fully Connected Layer
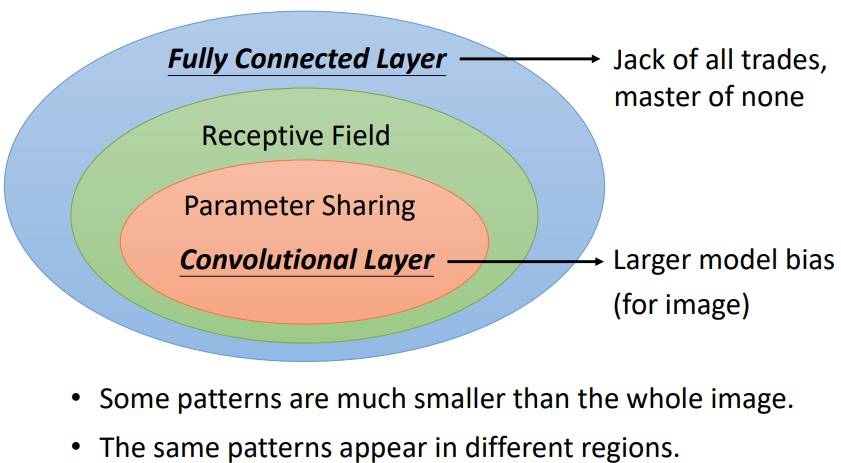
觀察:
- FC 可以通過“學習”決定要看到的“圖片”的範圍。加上“receptive field”概念後,就只能看某一個範圍
- FC 可以自由決定守備不同 receptive field 的各個神經元參數。加上“權值共享”概念後,守備不同 receptive field 的同一個 filter 參數相同
分析:
- 一般而言,model bias 小、model 的 flexibility 很高的時候,比較容易 overfitting。fully connected layer 可以有各式各樣的變化,但是它可能沒有辦法在任何特定的任務上做好
- CNN 的 bias 比較大,它是專門為影像設計的,所以它在影像上仍然可以做得好
3. 濾波器角度介紹 CNN
3.1 卷積層基本定義
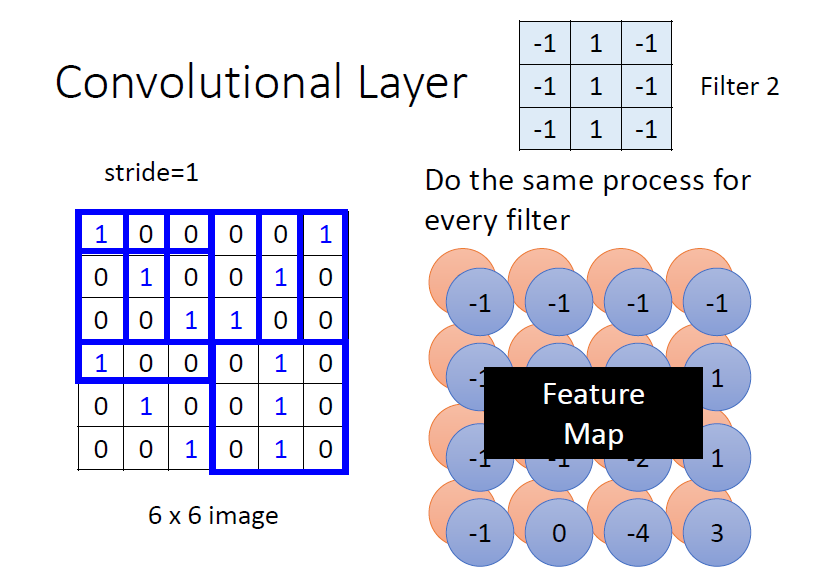
卷積層中有若干個 filters,每個 filter 可以“抓取”圖片中的某一種 pattern(pattern 的大小小於 receptive field 大小)。filter 的參數就是神經元中的“權值(weight)”
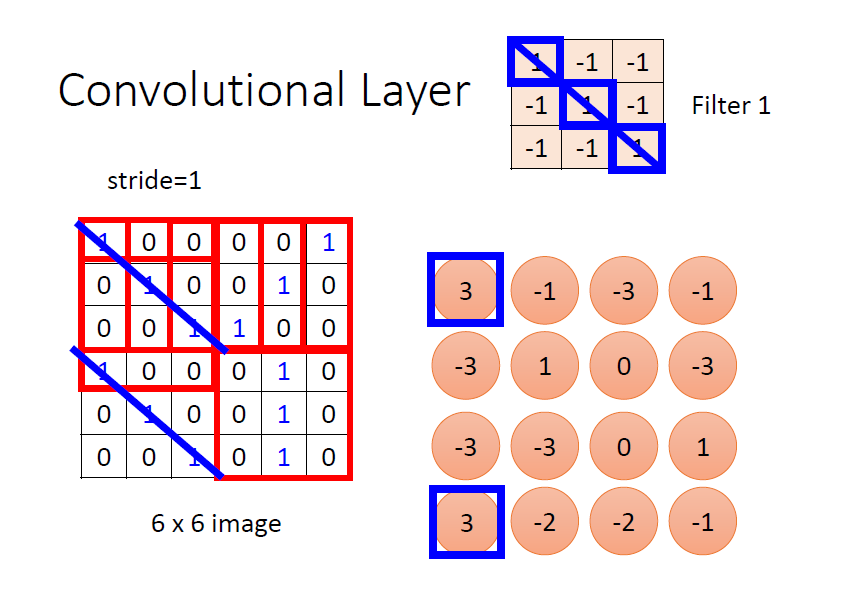
filter 的計算是“內積”:filter 跟圖片對應位置的數值做矩陣乘法,乘完後再將元素相加
注意:
上圖所示的濾波器,對主對角線為 1 的特徵敏感 ⇒ 對應卷積結果為 3(最大)
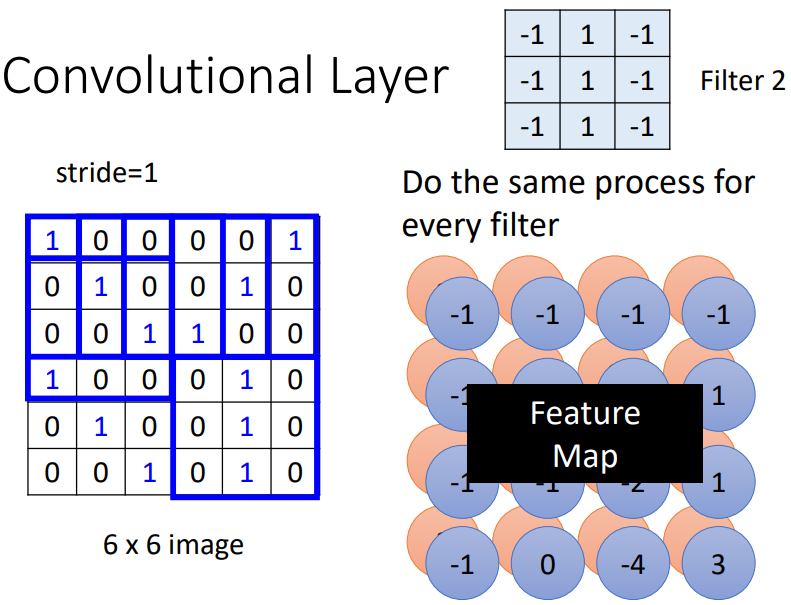
不同的 filter 掃過一張圖片,將會產生“新的圖片”,每個 filter 將會產生圖片中的一個 channel ⇒ feature map
3.2 多層卷積
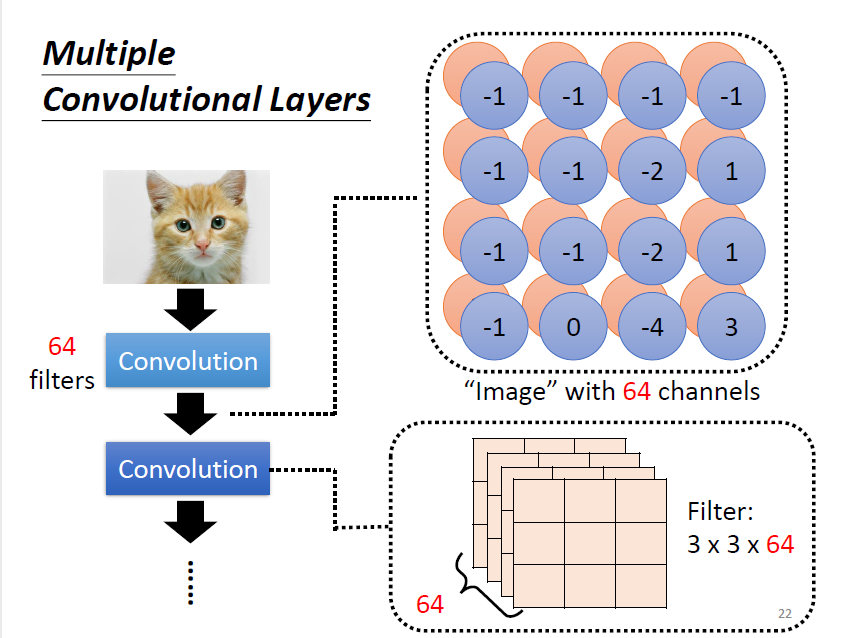
第一層的卷積結果產生了一張 的 feature map。繼續卷積時,需要對 64 個 channel 都進行處理 ⇒ filter 的“高度”要是 64
3.2.1 讓小卷積核看到大 pattern
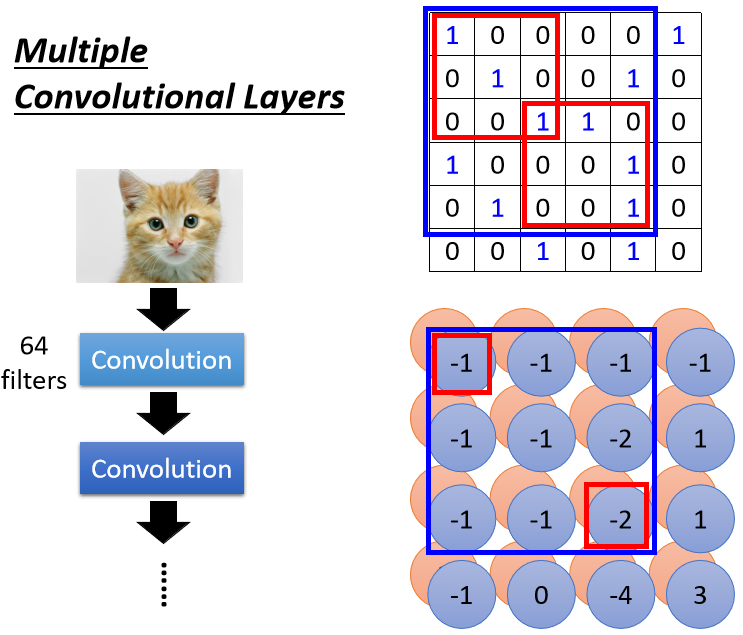
在考慮第二層中 的範圍,在原圖實際上考慮了 範圍的pattern。當卷積層越來越深時,即使只是 的 filter,看到的範圍實際上是會越來越大
4. 神經元角度(Neuron)vs 濾波器角度(Filter)
神經元角度說到 Neuron 會共用參數,這些共用的參數就是濾波器角度說到的 Filter
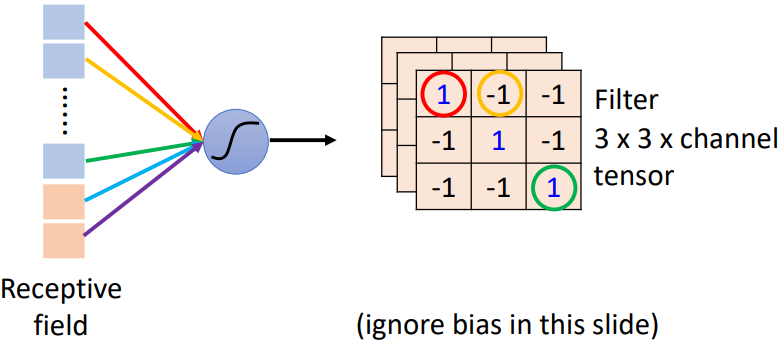

4.1 不用看整張圖片範圍
- 神經元角度:只要守備 receptive field
- 濾波器角度:使用 Filter 偵測模式 pattern
4.2 相同 Pattern 可能出現在圖片的不同位置
- 神經元角度:守備不同 receptive field 的神經元可以共用參數
- 濾波器角度:Filter 掃過整張圖片
5. Subsampling(Pooling)
舉例而言,把偶數行拿掉,把基數列拿掉,不會影響圖片的辨析,同時可以減少運算量

pooling 本身沒有參數,所以並不是一個 layer。行為類似於 activation function(sigmoid、ReLU ),是一個 operator,它的行為不是固定好的
5.1 不同 Pooling 方法
- Mean Pooling
- …
6. The whole CNN(典型 CNN 結構)
典型架構讓 convolution 及 pooling 交錯運用
Convolutional Layer → Pooling → ...(循環)→ Flatten(把矩陣拉直排成向量) → FC → Softmax
Pooling 可有可無
pooling 對於 rerformance 會帶來一點傷害。如果運算資源足夠,現今很多 network 的架構的設計往往就不做 pooling,改為全 convolution
7. 應用
7.1 Alpha Go
可使用 FC,但用 CNN 效果更好
把棋盤看成 的圖片,用 48 個 channel 來描述
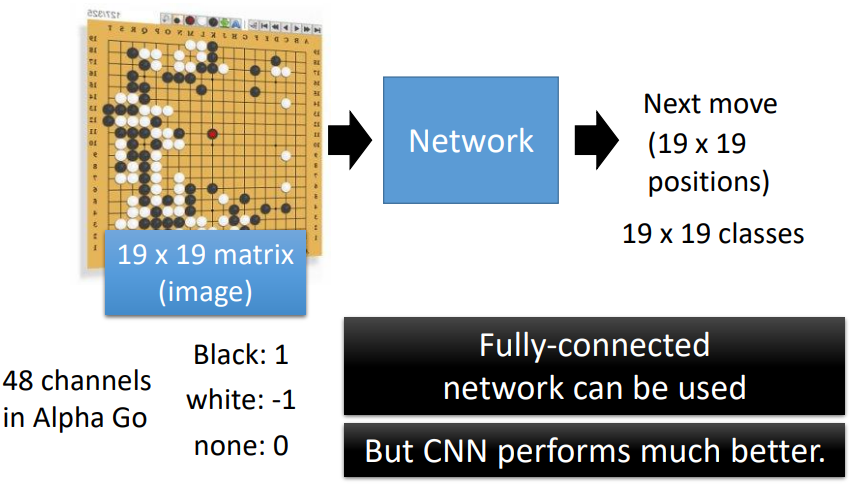
與圖像辨識的共同點
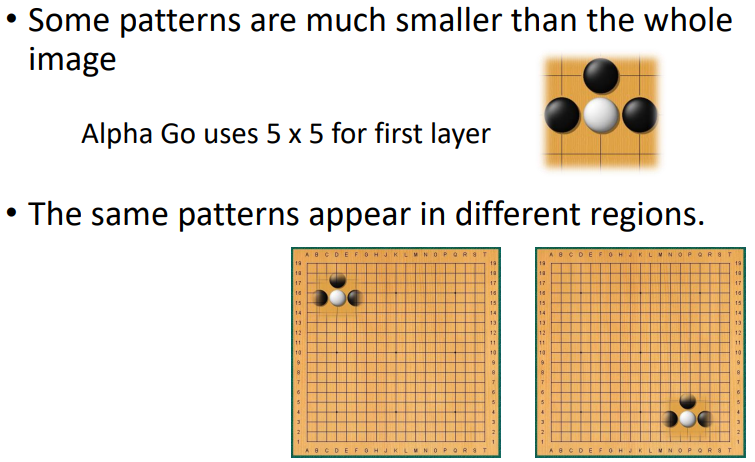
- 只看小範圍
- 同個 pattern 在不同位置出現
沒有 Pooling

7.2 語音、NLP
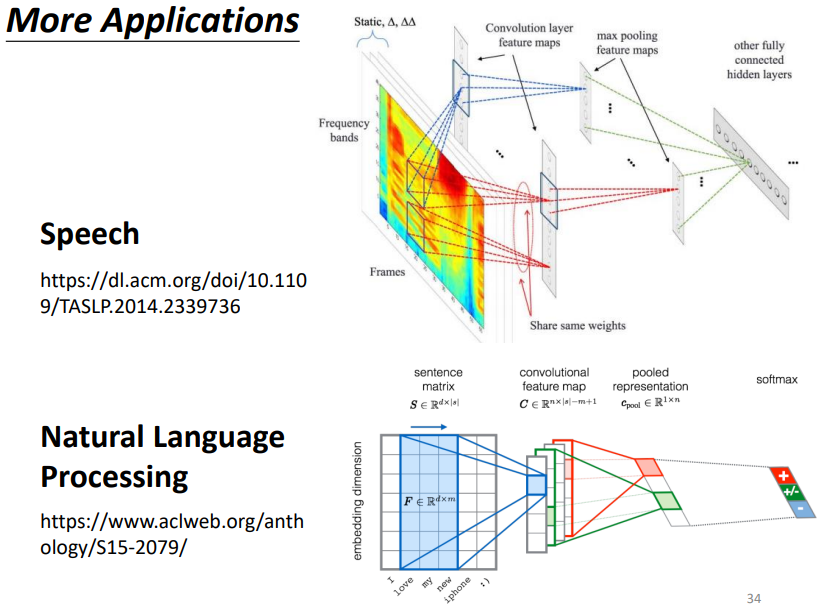
8. Learn More
CNN 的缺陷:
CNN 並不能夠處理影像放大縮小,或者是旋轉的問題。所以在做影像辨識的時候,往往都要做 data augmentation,把訓練數據截一小塊出來放大縮小、把圖片旋轉,CNN 才會做到好的結果
可以用 Spacial Transformer Layer 處理這個問題






