02.2-DeepLearning-類神經網路優化技巧
1. Critical Point
Critical Point 是梯度( gradient)為 0 的點
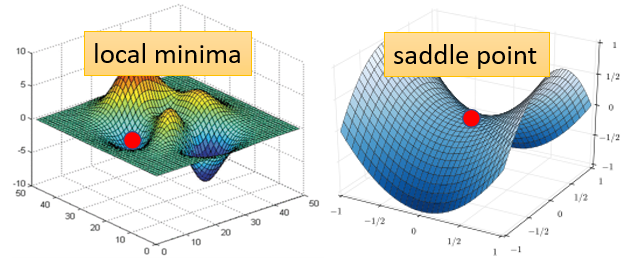
如果 loss 沒有辦法再下降,也許是因為卡在 critical point ⇒ local minima OR saddle point
- local minima:局部極小值
卡在 local minima,那可能就無路可走
- saddle point:鞍點
卡在 saddle point,旁邊還是有路可以走
1.1 如何判斷?
無法完整知道整個損失函數的樣子,但是如果給定某一組參數,比如 ,在 附近的損失函數是有辦法寫出來的,雖然 完整的樣子寫不出來 附近的 可近似為(泰勒級數展開):

- 第一項中,,當 跟 很近的时候, 很靠近
- 第二項中, 代表梯度,彌補 與 之間的差距; 的第 個 component 就是 的第 個 component 對 的偏微分
- 第三項中, 表示海森矩陣,是 的二階微分
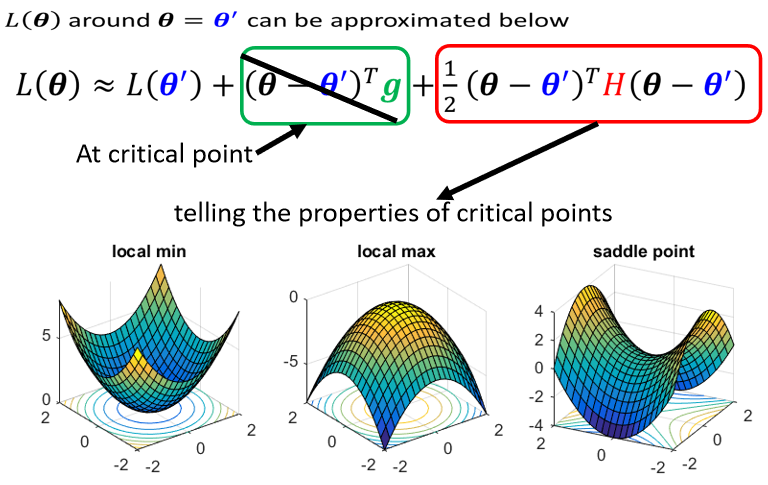
在 critical point 附近時:第二項為 0,根據第三項來判斷 → 只需考察 H 的特徵值

也可只算 就可
- 所有 eigen value 都是正的,H 是 positive definite(正定矩陣),此時是 local minima
- 所有 eigen value 都是負的,H 是 negative definite,此時是 local maxima
- 如果 eigen value 有正有負,代表是 saddle point
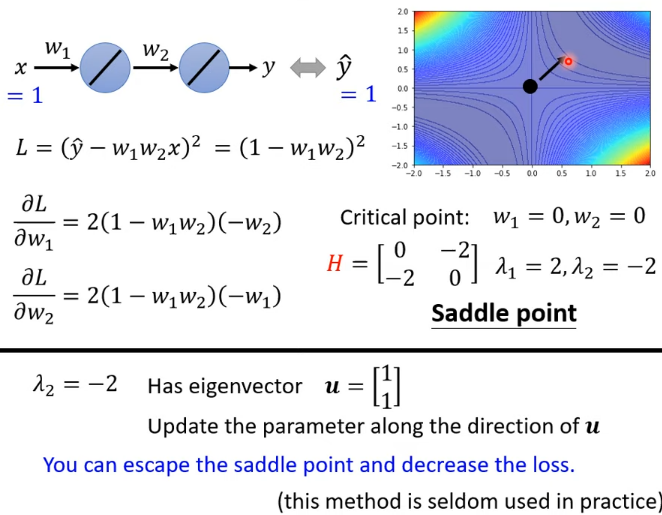
實例:
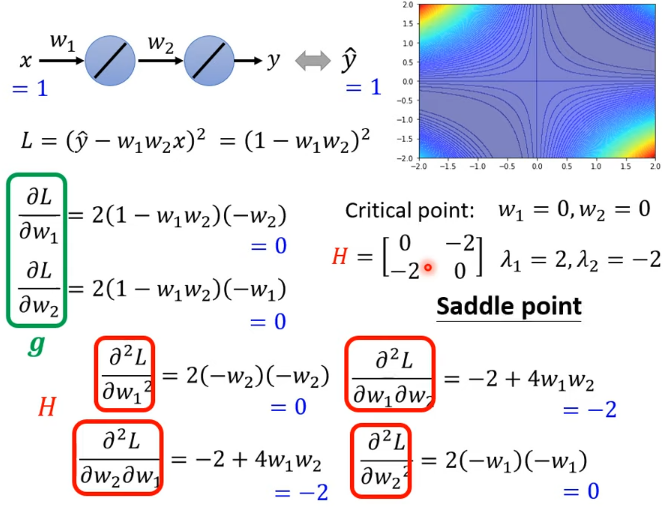
如果走到 saddle point,可以利用 的特徵向量確定參數的更新方向
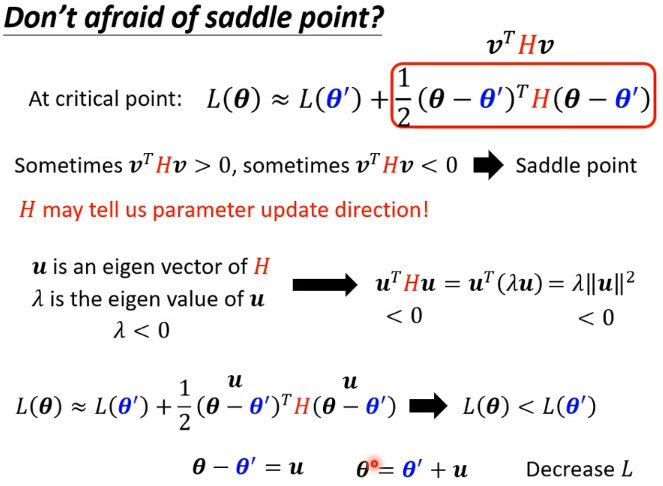
假設特徵值小於 0,得到對應的特徵向量 ,在 的位置加上 ,沿著 的方向做 update 得到 ,就可以讓 loss 變小
實例:
1.2 Local Minima 比 Saddle Point 少的多
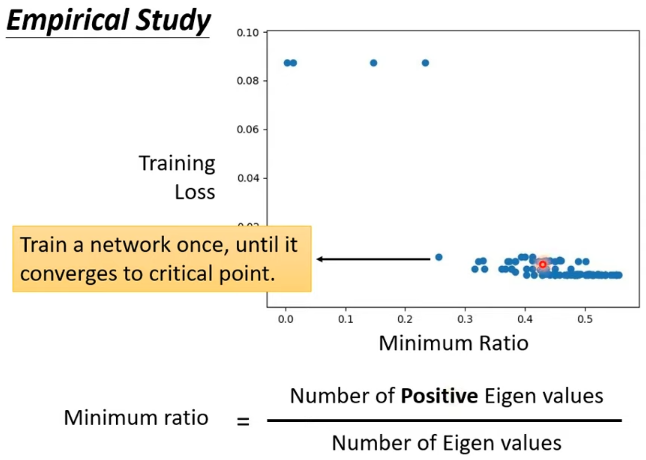
Loss 在一個維度很高的空間中,往往只會遇到鞍點而幾乎不會遇到局部極小值點
從上圖可以看出,正特徵值的數目最多只佔所有特徵值的 60%,這就說明剩餘 40%-50% 的維度都仍然“有路可走”(是 saddle point)
2. Batch and Momentum
2.1 Review:Optimization with Batch
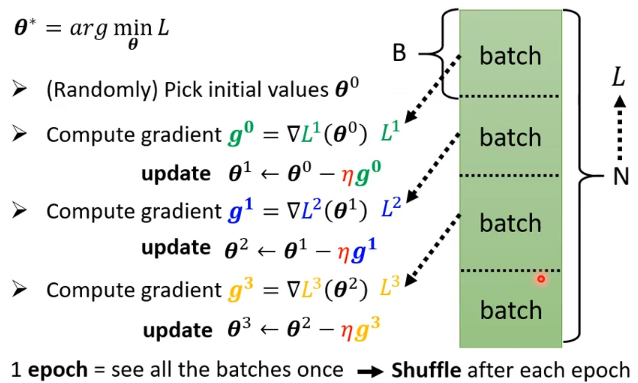
- 在 update 參數的時候,我們是拿 B 個樣本出來,算 loss、算 gradient
- 所有的 batch 看過一遍,叫做一個 epoch
Shuffle:
每個 Epoch 開始前往往會重新分一次 Batch,每一個 Epoch 的 Batch 都不一樣
2.2 Small Batch v.s. Large Batch
2.2.1 基本現象

- 左邊的 Case 必須要把所有 20 筆 examples 都看完以後,參數才能夠 update 一次
- 左邊蓄力時間長,但是威力比較大
- 右邊的 Case 只需要 1 筆樣本數據就 update 一次參數。用 1 筆資料算出來的 loss 顯然是比較 noisy,所以 update 的方向曲曲折折
- 右邊技能冷卻時間短,但是比較”不準”
2.2.2 時間性能
考慮並行運算,左邊(大的 batch size)並不一定時間比較長
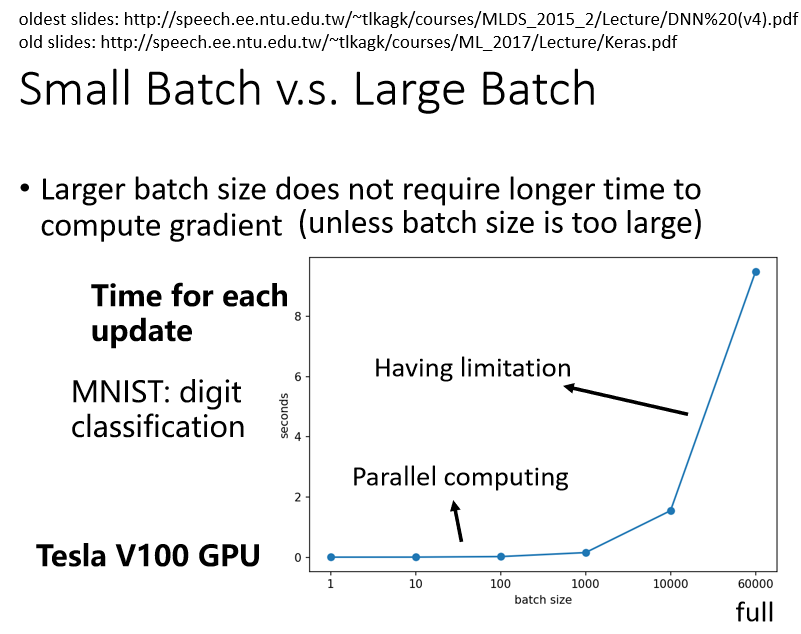
現象:
- batch size 是從 1 到 1000 所需要的時間幾乎是一樣的
- 增加到 10000 乃至增加到 60000 的時候,一個 batch 所要耗費的時間確實有隨著 batch size 的增加而逐漸增長,但影響不大
原因:
- 有 GPU,可以做並行運算,所以 1000 筆資料所花的時間,並不是 1 筆資料的 1000 倍
- GPU 平行運算的能力還是有極限,當 batch size 非常非常巨大的時,GPU 在跑完一個 Batch 並計算出 Gradient 所花費的時間,還是會隨著 batch size 的增加而逐漸增長
對總時間(1 epoch)的影響:
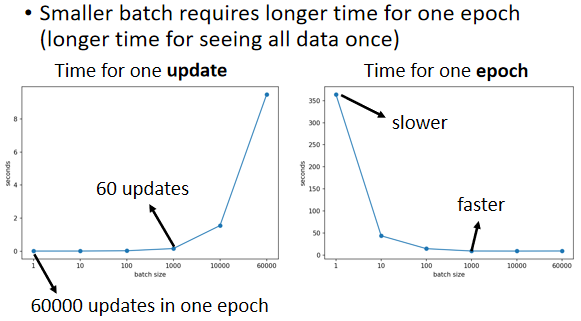
因為有平行運算的能力,因此實際上當 batch size 小的時候,要跑完一個 Epoch 花的時間比大的 batch size 還要多;反之,大的 batch size 下,跑完一個 Epoch 花的時間反而是比較少的
⇒ batch size 小時,Update 的次數大大增加
結論 1:使用較小的 Batch Size,在更新參數時會有 Noisy ⇒ 有利於訓練
不同的 batch 所用的 loss function 略有差異,可以避免局部極小值“卡住”
結論 2:使用較小的 Batch Size 可以避免 Overfitting(有利於測試)
根據 On Large-Batch Training For Deep Learning: Generalization Gap And Sharp Minima 這篇 paper 的實驗結果:可觀察出 training 的時候都很好,testing 時大的 batch 較小的 batch 結果差,代表 overfitting
一種解釋(尚待可以研究):
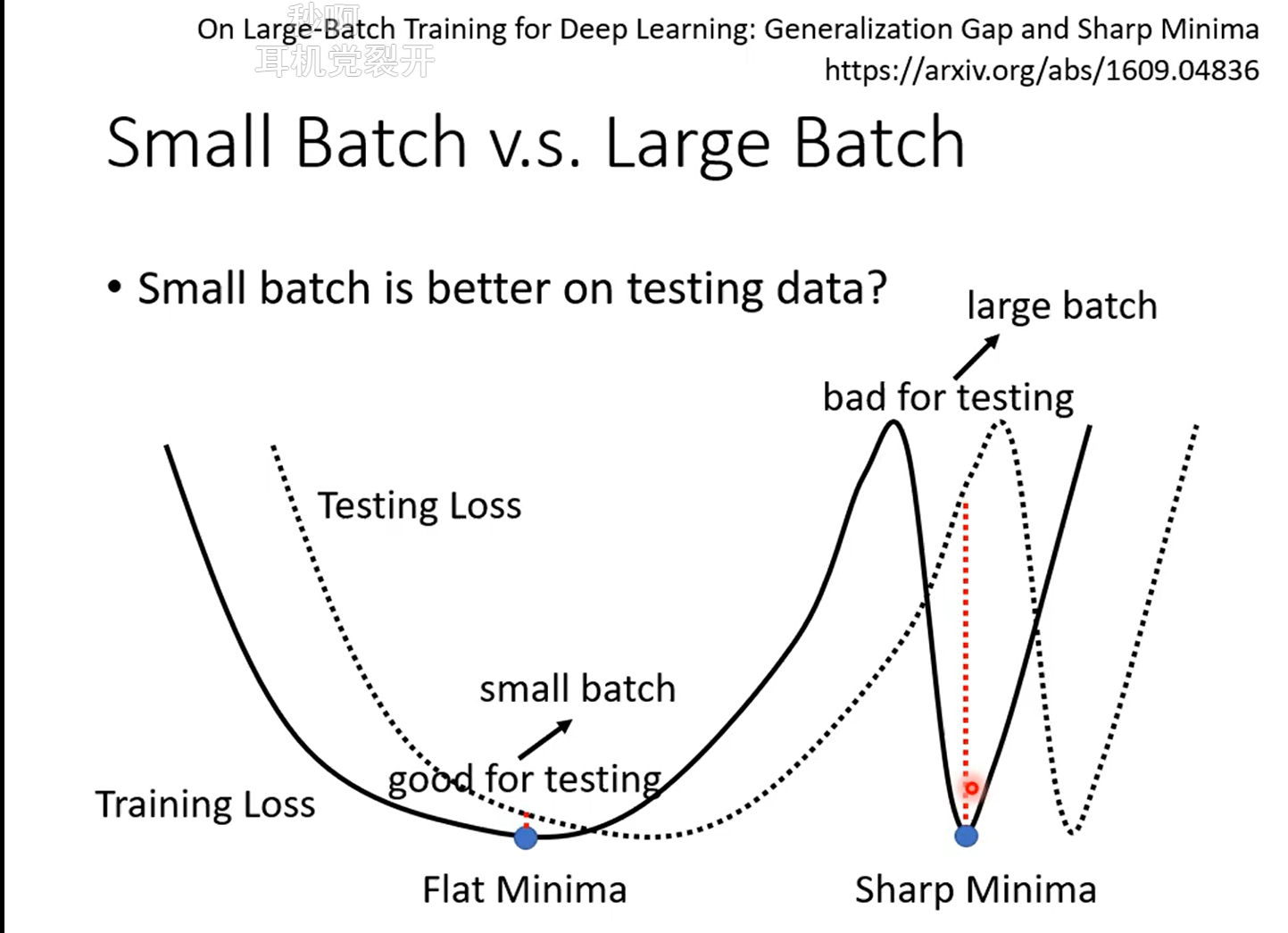
在一個峽谷裡面的 local minima 是壞的 minima;若在一個平原上的 local minima 是好的 minima
假設 testing 的 loss function 是把 training 的 loss function 往右平移
⇒ 對於在一個盆地裡面的 minima 來說,它的在 training 跟 testing 上面的結果不會差太多;但對於在峽谷裡面的 minima 來說,一差就可以天差地遠
大的 batch size,會傾向於走到峽谷裡面;而小的 batch size,傾向於走到盆地裡面
- 小的 batch 有很多的 loss,每次 update 的方向都不太一樣,如果這個峽谷非常地窄,有可能一個不小心就跳出去
- 大的 batch 是順著規定 update,它就很有可能走到一個比較小的峽谷裡面出不去
總結:Batch Size 是一個需要調整的參數,它會影響訓練速度與優化效果
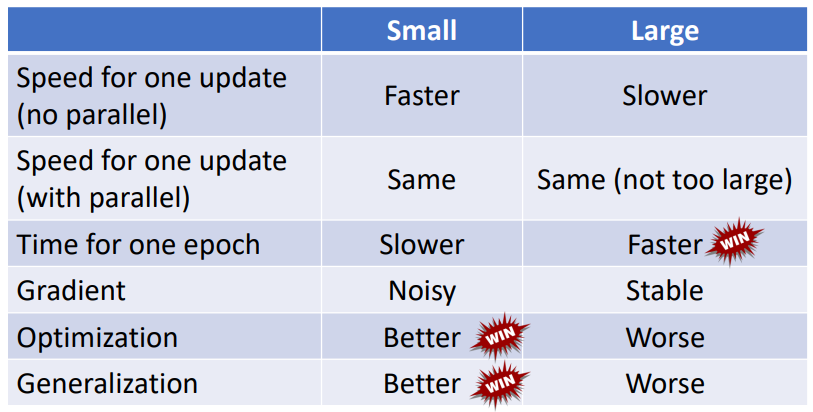
2.2.3 魚與熊掌兼得:結合大、小 Batch 的優點
2.3 Momentum
2.3.1 Vanilla Gradient Descent(一般的梯度下降)
只考慮梯度的方向,往反方向移動
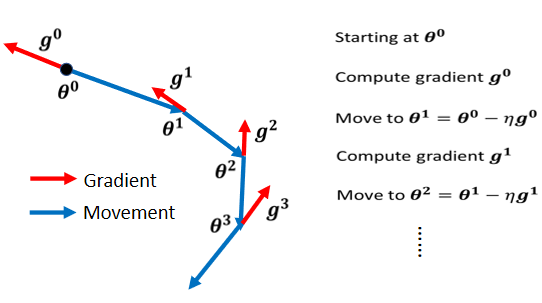
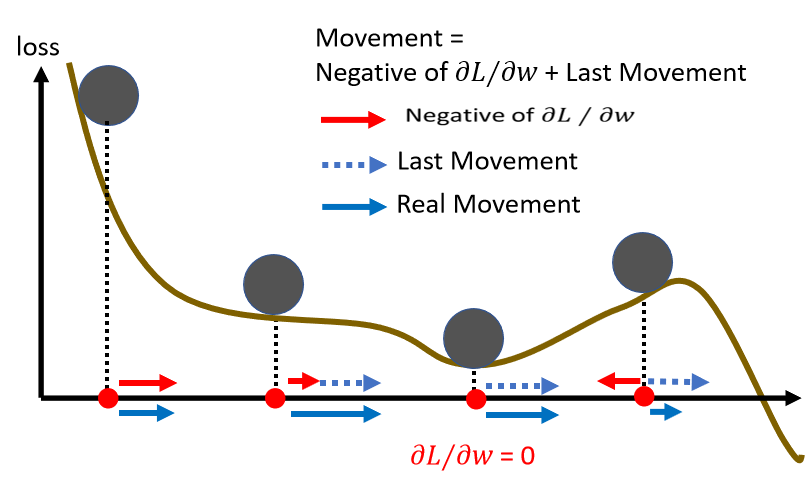
2.3.2 Gradient Descent + Momentum(考慮動量)
綜合梯度 + 前一步的方向
所謂的 momentum 就是 update 的方向不是只考慮現在的 gradient,而是考慮過去所有 gradient 的總合
2.4 總結
- critical points 梯度為 0
- saddle point 和 local minima 都屬於 critical point
- 可由 Hessian matrix 區分
- local minima 比較少遇到
- 可藉由沿 Hessian 矩陣的特徵向量方向離開 saddle point
- 較小的 batch size 和 momentum 可幫助離開 critical points
3. Adaptive Learning Rate
現象 1:
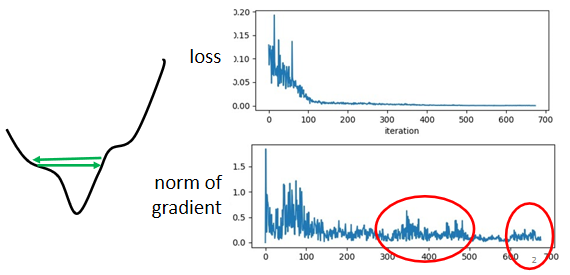
training stuck ≠ small gradient。loss 不再下降時,未必說明此時到達 critical point,梯度可能還很大。實際上走到 critical point 是一件很困難的事,有可能只是在山谷的谷壁間來回走
現象 2:
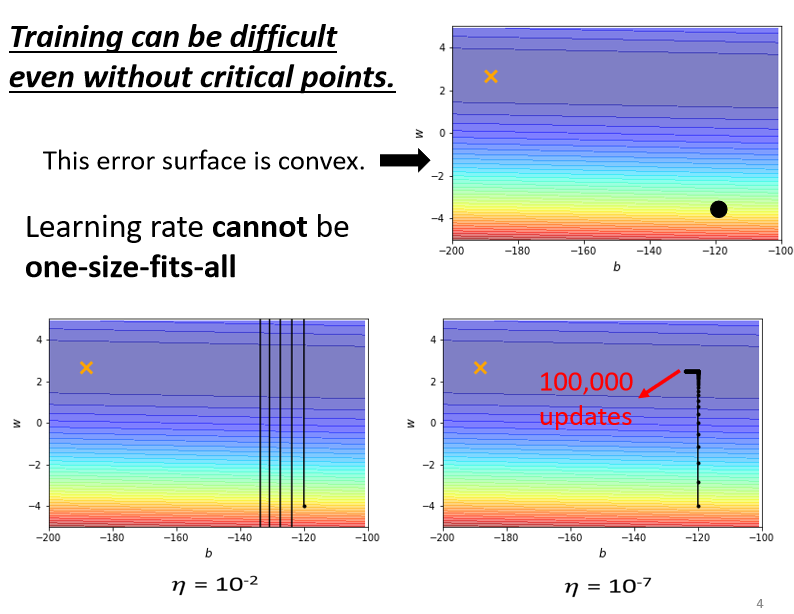
如果使用固定的學習率,即使是在凸面體的優化,都會讓優化的過程非常困難
- 較大的學習率:loss 在山谷的谷壁間震蕩而不會下降
- 較小的學習率:梯度較小時幾乎難以移動
3.1 客制化梯度
不同的參數(大小)需要不同的學習率,新增參數
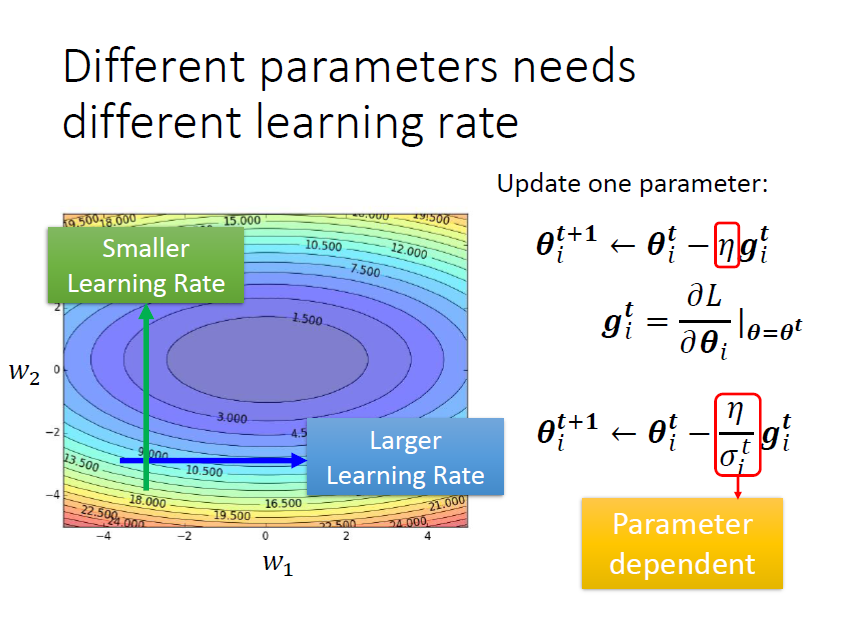
根據參數此時的實際情況,調整 的大小,實現對參數 的更新
基本原則:
- 某一個方向上 gradient 的值很小,非常的平坦 ⇒ learning rate 調大一點
- 某一個方向上非常的陡峭,坡度很大 ⇒ learning rate 可以設小一點
方法一:Adagrad
考慮之前所有的梯度大小
求取 的方式:
Root Mean Square(RMS),對本次及之前計算出的所有梯度求均方根
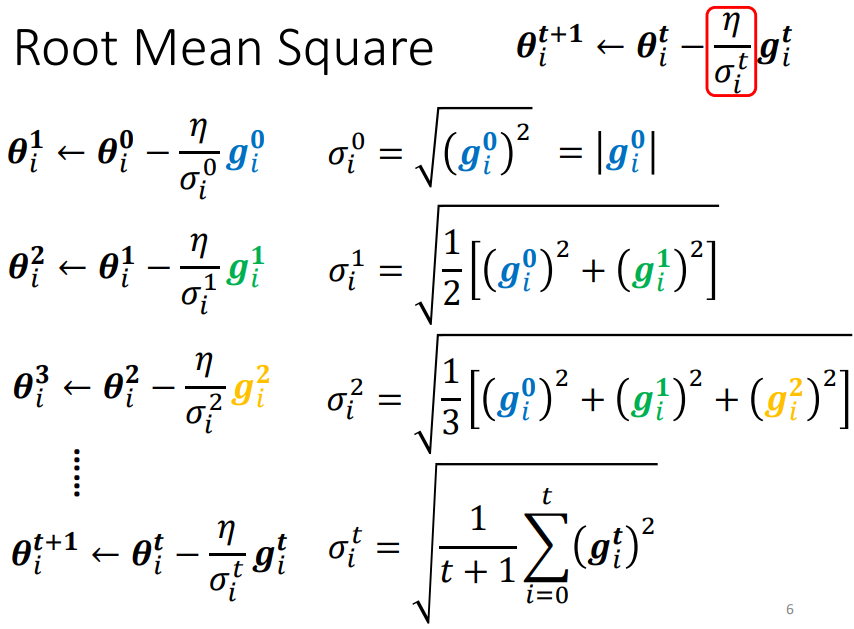
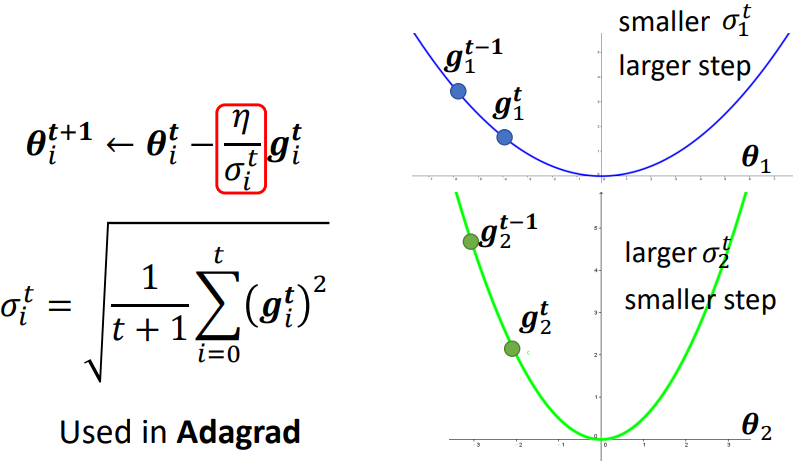
下面的坡度比較大 ⇒ gradient 較大 ⇒ σ 較大 ⇒ learning rate 小 ⇒ update 參數的量較小
缺點:
不能實時考慮梯度的變化情況
方法二:RMSProp
調整當前梯度與過去梯度的重要性
添加參數 ,越大說明過去的梯度訊息更重要
- α 設很小趨近於 0,代表過去的 gradient 較不重要,現在的 比較重要
- α 設很大趨近於 1,代表過去的 gradient 較重要,現在的 比較不重要
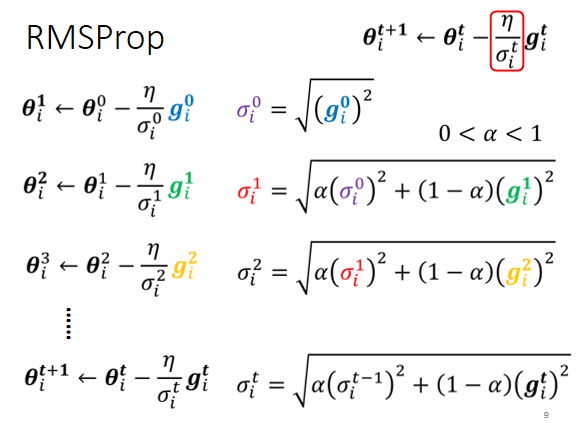
方法三:Adam = RMSProp + Momentum(最常用的策略)

使用 PyTorch 中預設的參數就能夠得到比較好的結果
3.2 Learning Rate Scheduling
讓 learning rate 與訓練時間有關
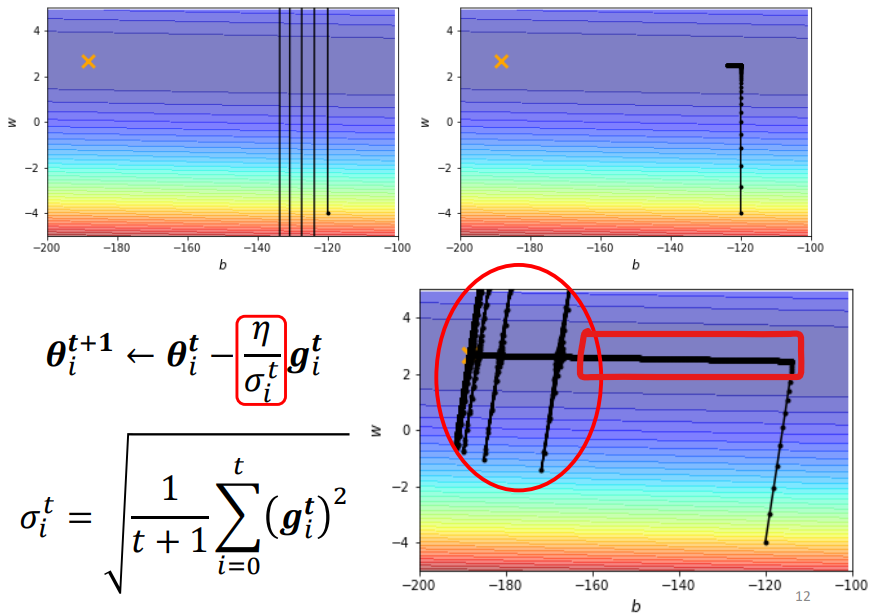
問題:
- 與右上圖相比,右下圖使用 Adagram 方法可以繼續往目標前進
- 紅色方框中累積了很小的 gradient,導致累積了很小的 σ,有突然暴增的情況
解決:
新增 ,讓它與時間有關
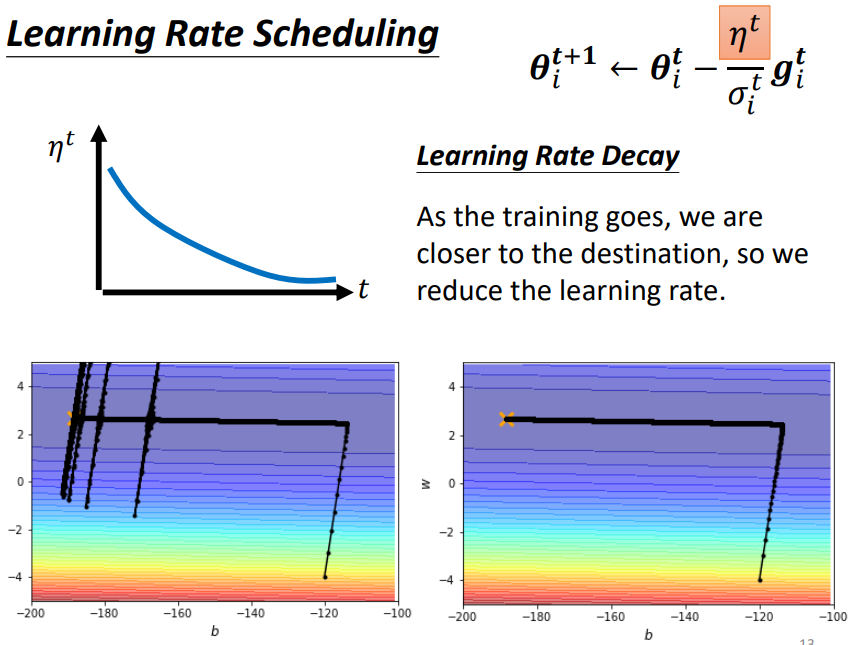
Learning Rate Decay:隨著時間的不斷地前進,隨著參數不斷的 update, 越來越小
Warm Up:讓 learning rate 先變大後再變小
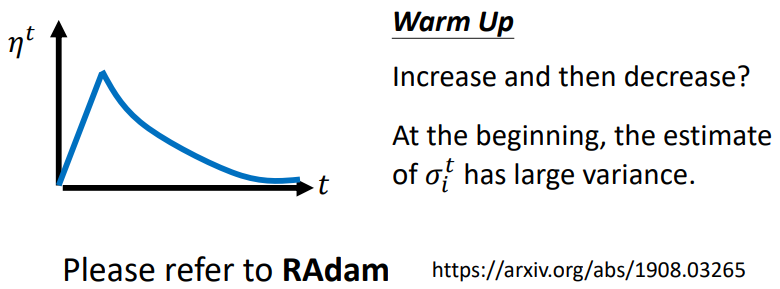
解釋:
指示某一個方向它到底有多陡/多平滑,這個統計的結果,要看得夠多筆數據以後才精準,所以一開始我們的統計是不精準的。一開始 learning rate 比較小,是讓它探索收集一些有關 error surface 的情報,在這一階段使用較小的 learning rate,限制參數不會走的離初始的地方太遠;等到 統計得比較精準以後再讓 learning rate 慢慢爬升
補充:RAdam 有更詳細的解釋 Warm Up
3.3 總結
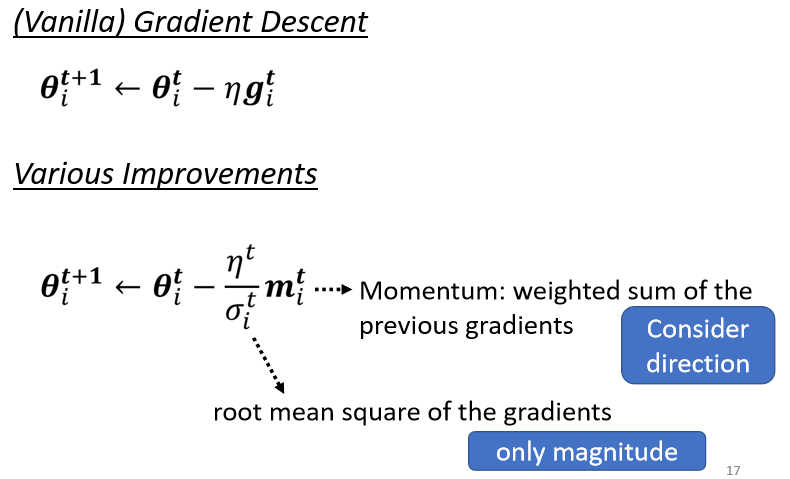
- 使用動量,考慮過去的梯度“大小”與“方向”
- 引入 ,考慮過去梯度的大小(RMS)
- 使用 learning rate schedule
3.4 Learn More
4. Batch Normalization
現象:
不同的參數發生變化,引起損失函數變化的程度不同,原因是因受不同維度輸入值的差異的影響
說明:
- 因 是乘上 , 當 的值很小時,參數 有變化時,使對 的影響很小,從而對 loss 的影響比較小
- 因 是乘上 , 當 的值很大時,參數 有變化時,使對 的影響很大,從而對 loss 的影響比較大
結論:
不同維度的輸入值 scale 差距可能很大,就會產生在不同方向上,斜率、坡度非常不同的 error surface
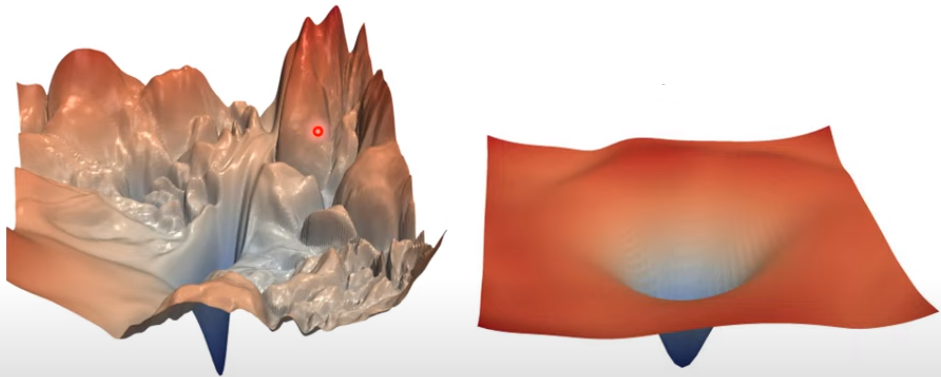
4.1 Feature Normalization(歸一化)
4.1.1 一種 Normalization 方法
對不同 feature 向量的同一維度進行標準化(Standardization)
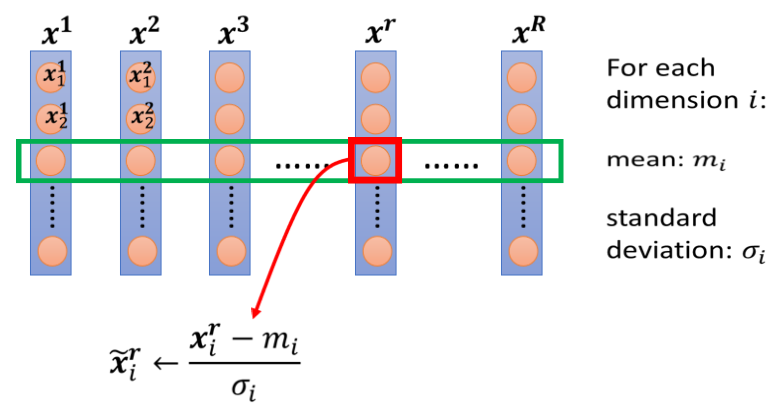
- 做完 normalize 後,這個 dimension 上面的數值平均為 0,variance 為 1,所以這一列數值的分布會都在 0 上下
- 對每一個 dimension 都做一樣的 normalization,就會發現所有 feature 不同 dimension 的數值都在 0 上下,就可以製造一個比較好的 error surface
4.1.2 每一層都需要一次 Normalization
經過 矩陣後, 數值的分布各維度仍然有很大的差異,要 train 第二層的參數 也會有困難,因此需要對 或者 進行 normalization
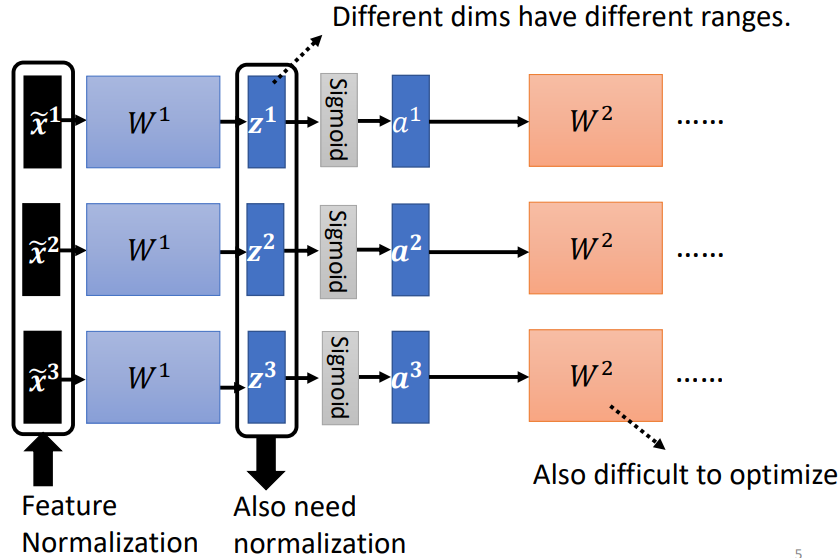
一般而言,normalization 步驟要放在 activation function 之前或之後都是可以的
如果選擇的是 sigmoid,比較推薦對 做 feature normalization。因為 Sigmoid 在 0 附近斜率比較大,所以如果對 做 feature normalization,把所有的值都挪到 0 附近,算 gradient 時,出來的值會比較大
具體步驟(對 做 Feature Normalization):
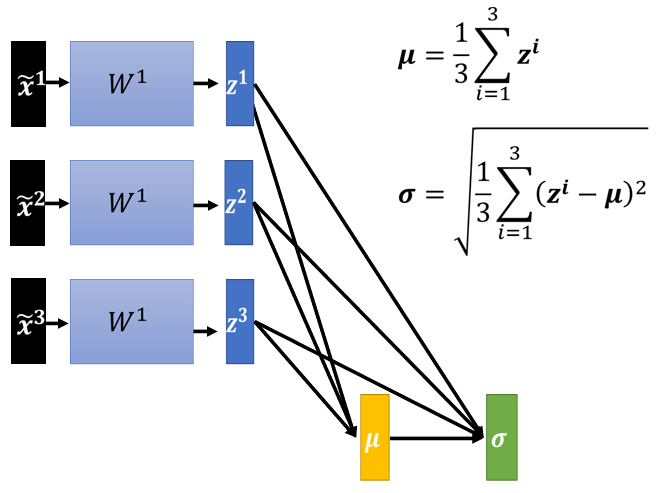
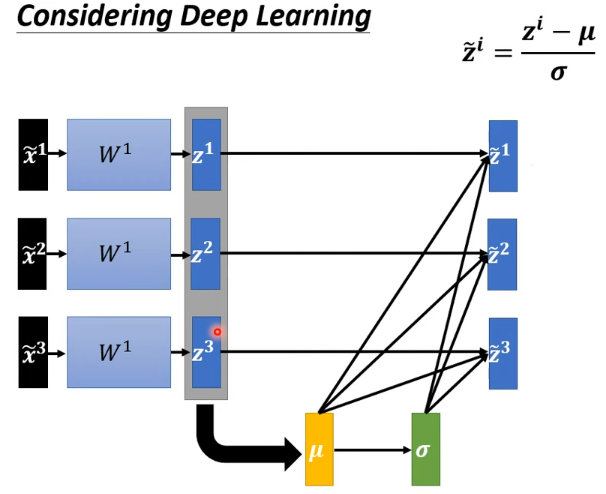
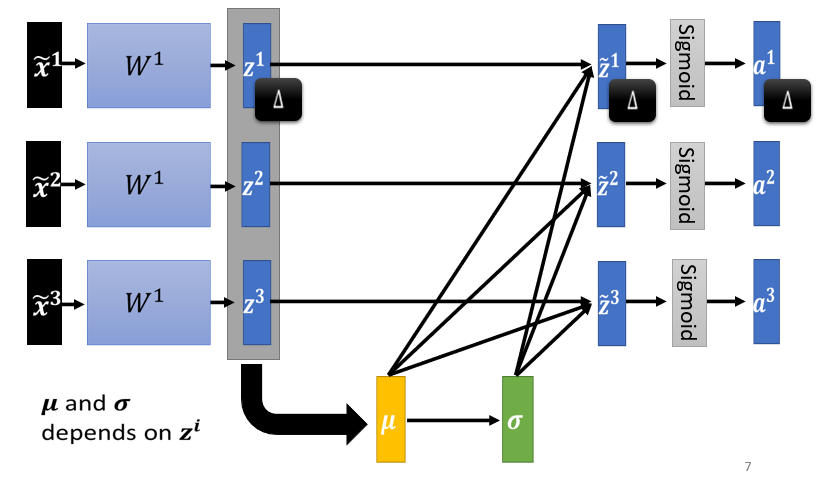
4.1.3 注意:對一批 數據進行歸一化
模型變為需一次處理一批 features 的模型,數據之間相互關聯
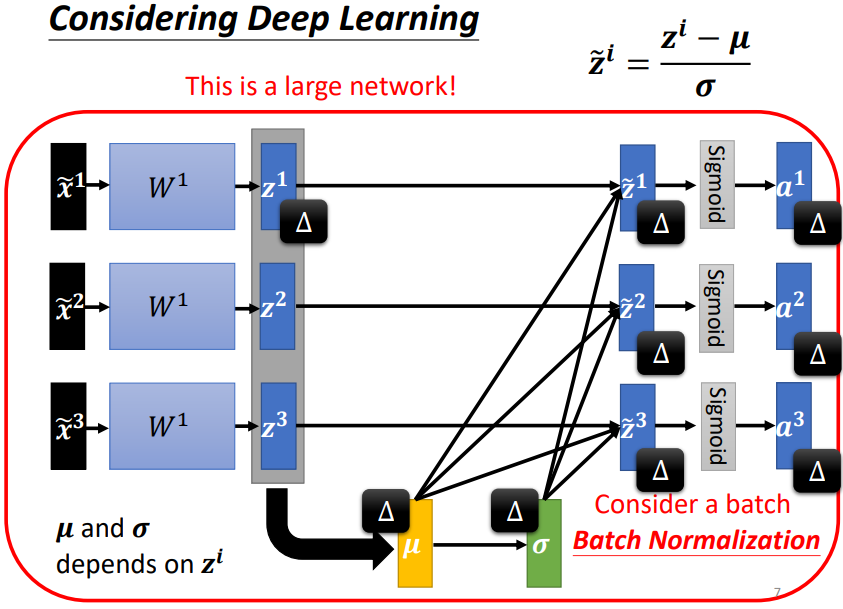
- 這μ 跟 都是根據 , , 算出來的,有做 feature normalization,當改變 的值時,μ 跟 也會跟著改變,當 μ 跟 改變後, 的值、 的值、 的值、 的值也會跟著改變
- 之前每一個 都是獨立分開處理的,但當做 feature normalization 後,這三個 feature 變得彼此關聯
- 之前的 network 都吃一個 feature 得到一個 output,現在有一個比較大的 network,這個 network 是吃一堆 features 用這堆 features 在這個 network 裡面,要算出 μ 跟 ,然後產生一堆 output
4.1.4 Batch Normalization
實際上做 normalization 時,只考慮有限數量的數據,即考慮一個 batch 內的數據,近似整個數據集
Batch Normalization 適用於 batch size 比較大。一個 batch 內的 data 可以認為足以表示整個 corpus 的分布,本來要對整個 corpus 做 feature normalization 這件事情,改成只在一個 batch 中做 feature normalization 作為近似
還原:
引入向量 ,將原本被歸一化到 的各維度資料恢復到某一分布
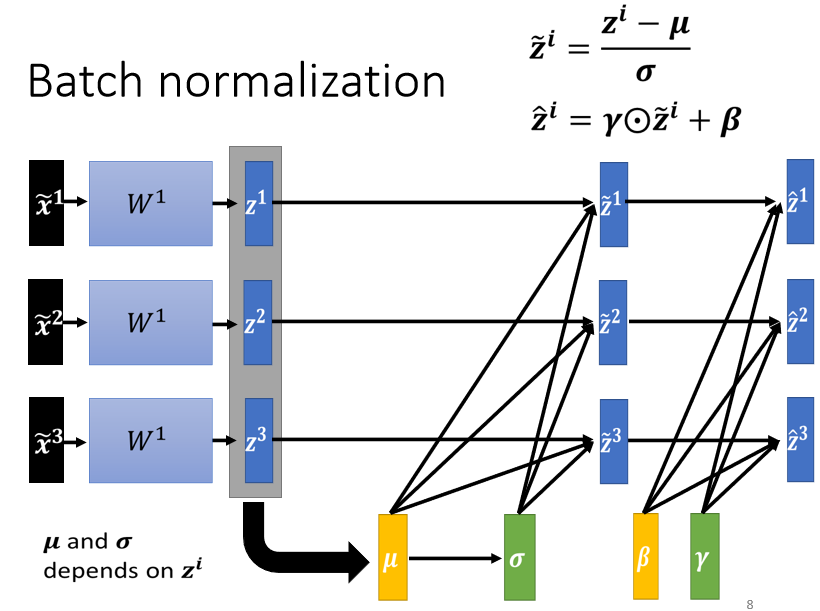
做 normalization 以後 平均就一定是 0,可以視作是給 network 一些限制,但這個限制可能會帶來負面的影響,因而增加 參數
訓練時初始將 設為全為 1 的向量, 設為全為 0 的向量。在一開始訓練的時,讓每一個 dimension 的分布比較接近。訓練夠長的一段時間,已經走到一個比較好的 error surface,那再把 慢慢地加進去
4.1.5 Testing 時會遇到的問題
testing(inference)時沒有 Batch 進行歸一化 ⇒ Training 時會紀錄 及
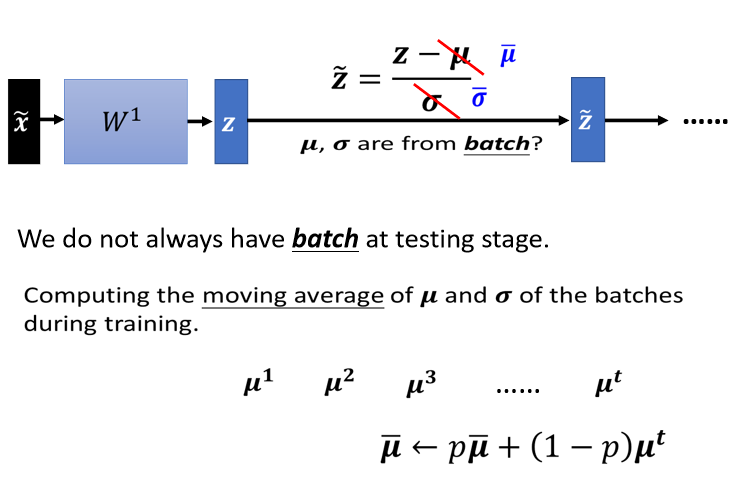
在 testing 階段一筆資料進來就要產生結果,沒有一個“batch”的數據可以進行歸一化,所以在 PyTorch 中,training 時就會把每一個 batch 計算出來的 跟 ,拿出來算 moving average
4.1.6 結果比較
紅色虛線(有做 Batch Normalization)收斂的速度顯然比黑色虛線(沒有做 Batch Normalization)要快很多
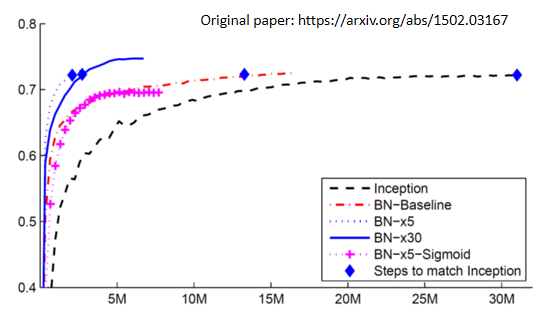
為什麼 Batch Normalization 會比較好?
在 How Does Batch Normalization Help Optimization 論文中,作者從實驗上,也從理論上,至少支持了 batch normalization 可以改變 error surface,讓 error surface 比較不崎嶇這個觀點
4.1.7 其他 Normalization 方法








