01-機器學習基本概念簡介

1. 機器學習的不同類型

機器學習就是讓機器具備找一個函式的能力

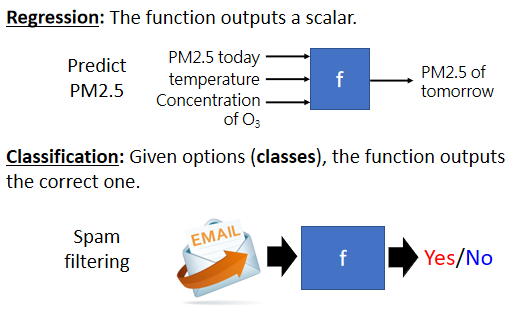
1.1 Regression

要找的函式，其輸出是一個數值

1.2 Classification

函式的輸出，就是從設定好的選項裡選擇一個當作輸出

1.3 Structured Learning

機器產生有結構的東西的問題，學會創造

2. Case Study：預測頻道流量

2.1 訓練三步驟

Step 1：Function with Unknown Parameters

$y$ 是要預測的東西

$x_1$ 是頻道前一天總觀看人數，跟 $y$ 一樣都是數值

$b$ 跟 $w$ 是未知的參數，透過準備資料找出最適合的參數
猜測：
未來點閱次數的函式 $f$ ，是前一天的點閱次數乘上 $w$ 再加上 $b$ 。猜測往往是對問題本質上的了解，是 domain knowledge

名詞定義：

Feature：function 中已知的訊息（ $x_1$ ）

Weight：未知參數，與 feature 直接相乘

Bias：未知參數，直接相加

Step 2：Define Loss from Training Data

loss 也是一個 function，它的輸入是 model 中的參數（ $w,b$ ）

物理意義：function 輸出的值代表，如果把這一組未知的參數設定某一個數值時，這筆數值好還是不好
L 越大，代表一組參數越不好，L 越小，代表現在這一組參數越好

計算方法：求取估測的值跟實際的值（label）之間的差距
- MAE（mean absolute error）
- MSE（mean square error）
- Cross-entropy：計算機率分布之間的差距

Error Surface：

試不同的參數，然後計算 loss 所畫出來的等高線圖

Step 3：Optimization

找到能讓損失函數值最小的參數

方法：

Gradient Descent（梯度下降）

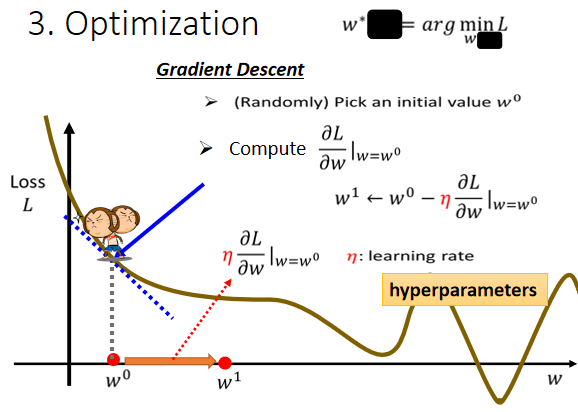
步驟：

隨機選取初始值 $w_0$

計算 $w=w_0$ 時， $w$  對 loss 的微分是多少

根據微分（梯度）的方向，改變參數的值
改變的大小取決於：
- 斜率的大小
- 學習率的大小（超參數）

什麽時候停下來？
1. 自己設置上限（超參數）
1. 理想情況：微分值為 0（極小值點），不會再更新 ⇒ 有可能陷入局部最小值，不能找到全局最小值
  事實上：局部最小值不是真正的問題！！！

推廣到多個參數：

2.2 Linear Model

根據周期性修改模型，考慮前7天，甚至更多天的值

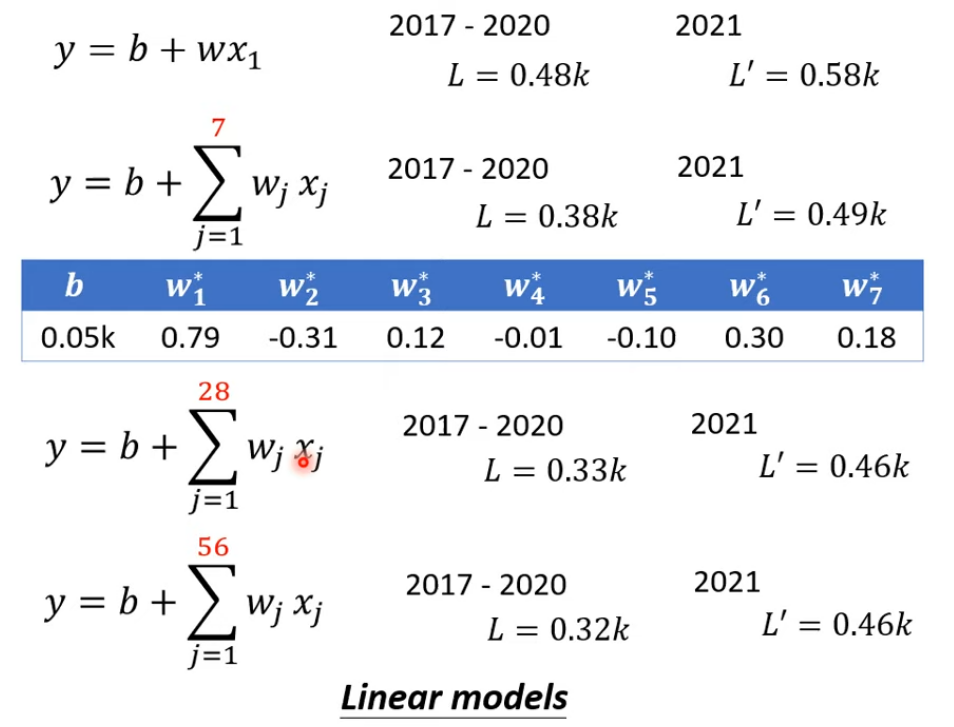
2.2.1 Model Bias

問題：

模型遇到無法模擬或描述真實情況的狀況

解決：

需要一個更複雜的、更有彈性的、有未知參數的 function

2.3 Piecewise Linear Curves（Sigmoid）

2.3.1 模型定義

定義：

由多段鋸齒狀的線段所組成的線，可以看作是一個常數，再加上若干個藍色的 function（Hard Sigmoid）

y=b+\sum_isigmoid(b_i+w_ix_i)

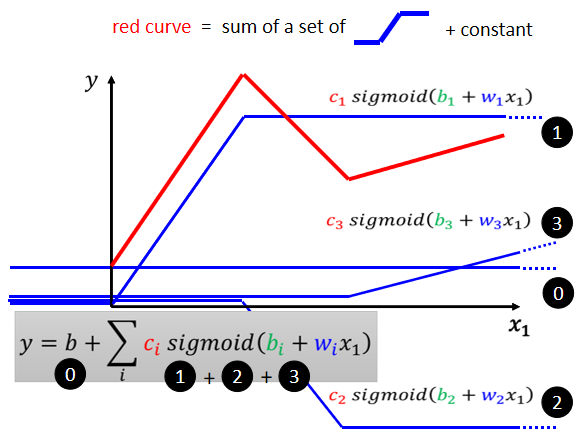
用一條曲線來近似描述這條藍色的曲線：Sigmoid 函數（S 型的 function）

事實上，sigmoid 的個數就是神經網絡中的一層的 neuron 節點數（使用幾個 sigmoid 是超參數）

結論：

可以用 Piecewise Linear 的 Curves，去逼近任何的連續的曲線

每一個 Piecewise Linear 的 Curves，都可以用一大堆藍色的 Function 加上一個常量組合起來得到

只要有足夠的藍色 Function 把它加起來，就可以變成任何連續的曲線

2.3.2 Sigmoid 函數

Sigmoid：y = c\frac{1}{{1+e^{-(b+wx_1)}}}

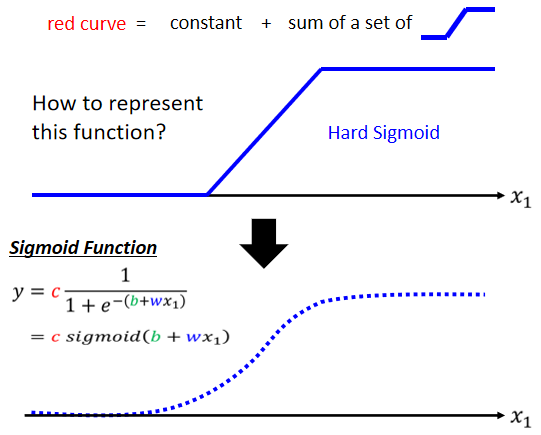
$x_1$ 趨近於正無窮大 ⇒ 收斂於高度 $c$

$x_1$ 負非常大，分母就會非常大 ⇒ $y$ 值趨近於 0

調整 $w,b,c$ ，可以得到各種不同的 sigmiod 來逼近”藍色function“，通過求和，最終近似各種不同的 continuous function

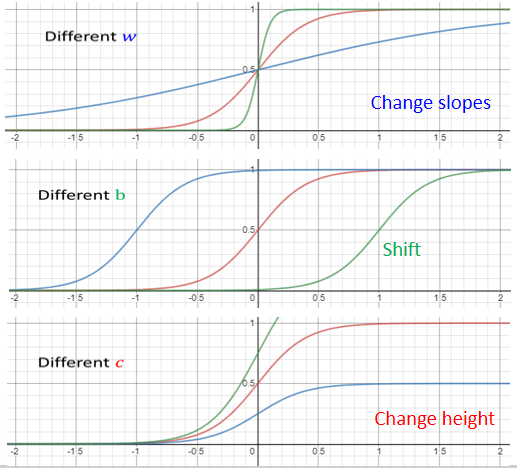
如果改 $w$ ，就會改變斜率，改變斜坡的坡度

如果改 $b$ ，就可以把 sigmoid function 左右移動

如果改 $c$ ，就可以改變它的高度

總結：

利用若干個具有不同 $w,b,c$ 的 Sigmoid 函數與一個常數參數的組合，可以模擬任何一個連續的曲線（非線性函數）

擴展到多個特徵：

y=b+\sum_isigmoid(b_i+\sum_j(w_{ij}x_j))

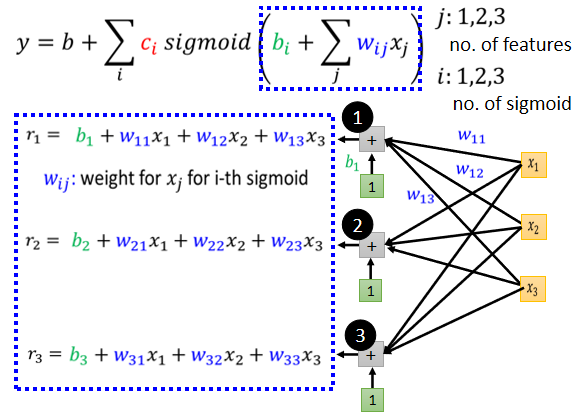
$j$ 等於 1 2 3， $x_1$ 代表前一天的觀看人數， $x_2$ 兩天前觀看人數， $x_3$ 三天前的觀看人數

每一個 $i$ 就代表了一個藍色的 function，現在每一個藍色的 function 都用一個 sigmoid function 來近似它

$w_{ij}$ 第 $i$ 個 sigmoid 給第 $j$ 個 feature 的權重

轉化為矩陣計算 + 激勵函數形式：

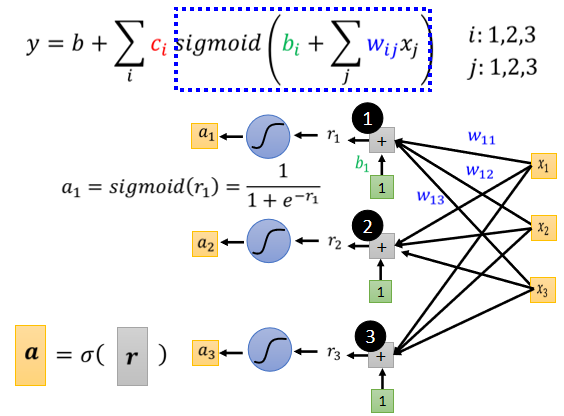
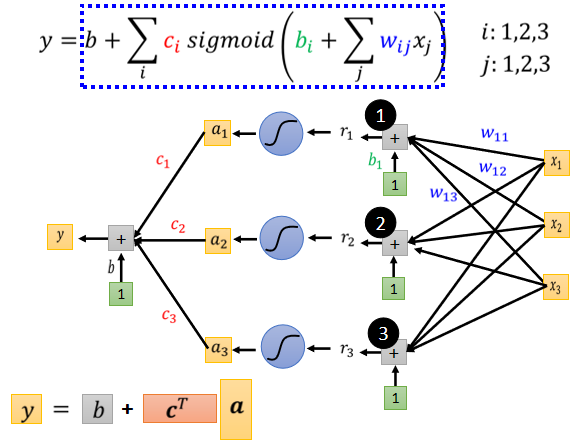
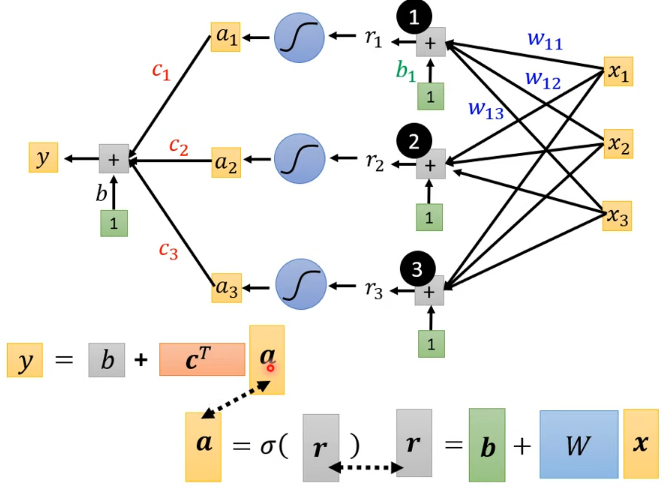
總之：

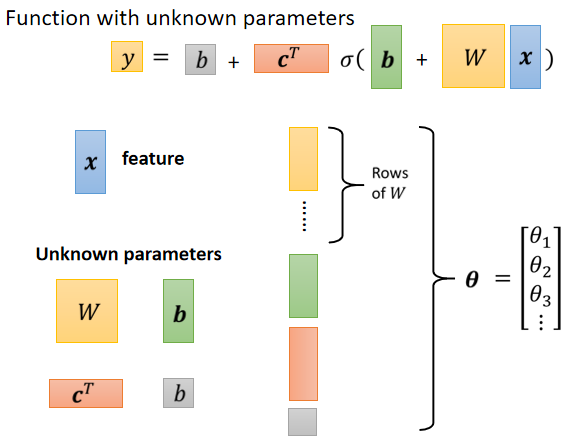
一般來說，將所有參數統稱為 $\theta$ （包含 $W,\vec{b} ,b$ ...)

2.3.3 Loss 函數

因為所有參數統稱為 $\theta$ ，loss 表示為 $L(\theta)$

2.3.4 優化過程

仍是梯度下降

（1）選定初始參數值（向量） $\theta_0$

（2）對每個參數求偏微分

（3）更新參數，直至設定的次數

▲ Batch training

每次更新參數時，只使用 1 個 batch 裡的資料計算 loss，求取梯度，更新參數

batch 大小也是超參數

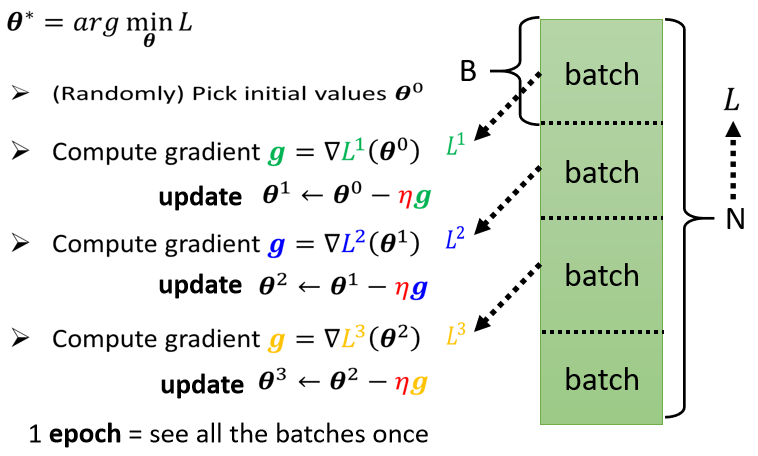
Update：每次更新一次參數叫做一次 Update

Epoch：把所有 batch 都看過一遍叫做一個 Epoch

2.4 ReLU

把兩個 ReLU 疊起來就等於 hard sigmoid

y=b+\sum_imax(0, b_i+w_ix_i)

Sigmoid 和 ReLU 都屬於激勵函數（Activation Function）

▲ 模型變型 ⇒ 多加幾層

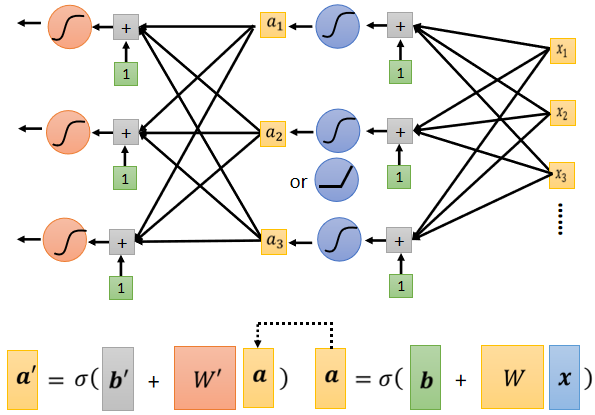
3. 引入 Deep Learning

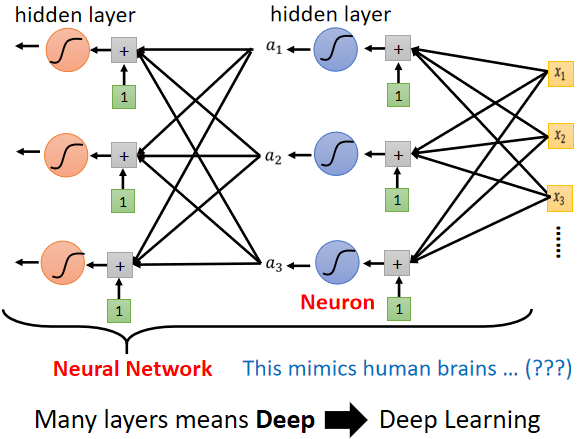
問題：

為什麽要“深”，而不“胖”？

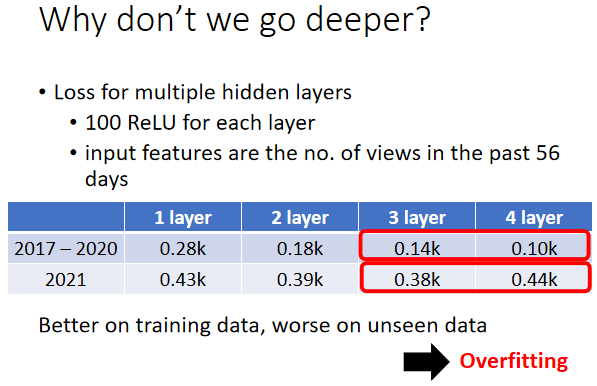
Overfitting：在訓練資料上有變好，但是在沒看過的資料上沒有變好

4. Learn More